Chapter 13 Nested case-control study and case-cohort study: Risk factors of coronary heart disease

In this exercise we shall apply both the nested case-control (NCC) design and the case-cohort (CC) design in sampling control subjects from a defined cohort or closed study population. The case group comprises those cohort members who die from coronary heart disease (CHD) during a \(> 20\) years follow-up of the cohort.
The risk factors of interest are cigarette smoking, systolic blood pressure, and total cholesterol level.

Our study population is an occupational cohort comprising 1501 men working in blue-collar jobs in one Nordic country. Eligible subjects had no history of coronary heart disease when recruited to the study in the early 1990s. Smoking habits and many other items were inquired at baseline by a questionnaire, and blood pressure was measured by a research nurse, the values being written down on the questionnaire. Serum samples were also taken from the cohort members at the same time and were stored in a freezer. For some reason, the data in the questionnaires were not entered to any computer file, but the questionnaires were kept in a safe storehouse for further purposes. Also, no biochemical analyses were initially performed for the sera collected from the participants. However, dates of birth and dates of entry to the study were recorded in an electronic file.

In 2010 the study was suddenly reactivated by those investigators of the original team who were still alive then. As the first step mortality follow-up of the cohort members was executed by record linkage to the national population register, from which the dates of death and emigration were obtained. Another linkage was performed with the national register of causes of death in order to get the deaths from coronary heart disease identified. As a result a data file occoh.txt was completed containing the following variables:

Variable Description
id identification number
birth date of birth
entry date of recruitment and baseline measurements
exit date of exit from mortality follow-up
death indicator for vital status at the end of follow-up; 1, if dead from any cause, and = 0, if alive
chdeath indicator for death from coronary heart disease; 1, if yes, and 0, if no.

This exercise is divided into five main parts:

  1. Description of the study base or the follow-up experience of the whole cohort, identification of the cases and illustrating the risk sets.

  2. Nested case-control study within the cohort:

    1. selection of controls by risk set or time-matched sampling using function ccwc() in package Epi,
    2. collection of exposure data for cases and controls from the pertinent data base of the whole cohort to the case-control data set using function merge(), and
    3. analysis of the case-control data set with stratified Cox model using function clogit() in package survival(),

  3. Case-cohort study within the cohort:

    1. selection of a subcohort by simple random sampling from the cohort,
    2. collection of exposure data for subcohort members and cases, and
    3. analysis of the case-cohort data set with Cox model by weighted partial likelihood including appropriate weighting and correction of estimated covariance matrix for the model coefficients using function cch() in package survival().

  4. Comparison of results from all previous analyses, also with those from a full cohort design.

  5. Further tasks and homework.

13.1 Reading the cohort data, illustrating the study base and risk sets

  • Load the packages Epi and survival. Read in the cohort data file and name the resulting data frame as oc. See its structure and print the univariate summaries.
library(Epi)
library(survival)
url <- "https://raw.githubusercontent.com/SPE-R/SPE/master/pracs/data"
oc <- read.table(paste(url, "occoh.txt", sep = "/"), header = TRUE)
str(oc)
## 'data.frame':    1501 obs. of  6 variables:
##  $ id     : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ birth  : chr  "1943-02-19" "1934-07-06" "1939-03-05" "1939-07-03" ...
##  $ entry  : chr  "1990-08-14" "1990-08-14" "1990-08-14" "1990-08-14" ...
##  $ exit   : chr  "2009-12-31" "2009-12-31" "2009-12-31" "2009-12-31" ...
##  $ death  : int  0 0 0 0 1 1 1 1 0 0 ...
##  $ chdeath: int  0 0 0 0 0 0 0 1 0 0 ...
summary(oc)
##        id          birth              entry               exit          
##  Min.   :   1   Length:1501        Length:1501        Length:1501       
##  1st Qu.: 376   Class :character   Class :character   Class :character  
##  Median : 751   Mode  :character   Mode  :character   Mode  :character  
##  Mean   : 751                                                           
##  3rd Qu.:1126                                                           
##  Max.   :1501                                                           
##      death           chdeath       
##  Min.   :0.0000   Min.   :0.00000  
##  1st Qu.:0.0000   1st Qu.:0.00000  
##  Median :0.0000   Median :0.00000  
##  Mean   :0.1972   Mean   :0.07995  
##  3rd Qu.:0.0000   3rd Qu.:0.00000  
##  Max.   :1.0000   Max.   :1.00000
  • It is convenient to change all the dates into fractional calendar years
oc$ybirth <- cal.yr(oc$birth)
oc$yentry <- cal.yr(oc$entry)
oc$yexit <- cal.yr(oc$exit)

We shall also compute the age at entry and at exit, respectively, as age will be the main time scale in our analyses.

oc$agentry <- oc$yentry - oc$ybirth
oc$agexit <- oc$yexit - oc$ybirth
  • As the next step we shall create a lexis object from the data frame along the calendar period and age axes, and as the outcome event we specify the coronary death.
oc.lex <- Lexis(
  entry = list(
    per = yentry,
    age = yentry - ybirth
  ),
  exit = list(per = yexit),
  exit.status = chdeath,
  id = id, data = oc
)
## NOTE: entry.status has been set to 0 for all.
str(oc.lex)
## Classes 'Lexis' and 'data.frame':    1501 obs. of  17 variables:
##  $ per    : 'cal.yr' num  1991 1991 1991 1991 1991 ...
##  $ age    : 'cal.yr' num  47.5 56.1 51.4 51.1 55.5 ...
##  $ lex.dur: 'cal.yr' num  19.4 19.4 19.4 19.4 15.6 ...
##  $ lex.Cst: num  0 0 0 0 0 0 0 0 0 0 ...
##  $ lex.Xst: int  0 0 0 0 0 0 0 1 0 0 ...
##  $ lex.id : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ id     : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ birth  : chr  "1943-02-19" "1934-07-06" "1939-03-05" "1939-07-03" ...
##  $ entry  : chr  "1990-08-14" "1990-08-14" "1990-08-14" "1990-08-14" ...
##  $ exit   : chr  "2009-12-31" "2009-12-31" "2009-12-31" "2009-12-31" ...
##  $ death  : int  0 0 0 0 1 1 1 1 0 0 ...
##  $ chdeath: int  0 0 0 0 0 0 0 1 0 0 ...
##  $ ybirth : 'cal.yr' num  1943 1935 1939 1940 1935 ...
##  $ yentry : 'cal.yr' num  1991 1991 1991 1991 1991 ...
##  $ yexit  : 'cal.yr' num  2010 2010 2010 2010 2006 ...
##  $ agentry: 'cal.yr' num  47.5 56.1 51.4 51.1 55.5 ...
##  $ agexit : 'cal.yr' num  66.9 75.5 70.8 70.5 71.1 ...
##  - attr(*, "time.scales")= chr [1:2] "per" "age"
##  - attr(*, "time.since")= chr [1:2] "" ""
##  - attr(*, "breaks")=List of 2
##   ..$ per: NULL
##   ..$ age: NULL
summary(oc.lex)
##     
## Transitions:
##      To
## From    0   1  Records:  Events: Risk time:  Persons:
##    0 1381 120      1501      120   25280.91      1501
  • At this stage it is informative to examine a graphical presentation of the follow-up lines and outcome cases in a conventional Lexis diagram. Make use of the plot method for Lexis objects. Gray lifelines are drawn and a bullet is put at the exit point of those lifelines that end with the outcome event.
par(mfrow = c(1, 1))
plot(oc.lex, xlim = c(1990, 2010), grid = TRUE)
points(oc.lex, pch = c(NA, 16)[oc.lex$lex.Xst + 1])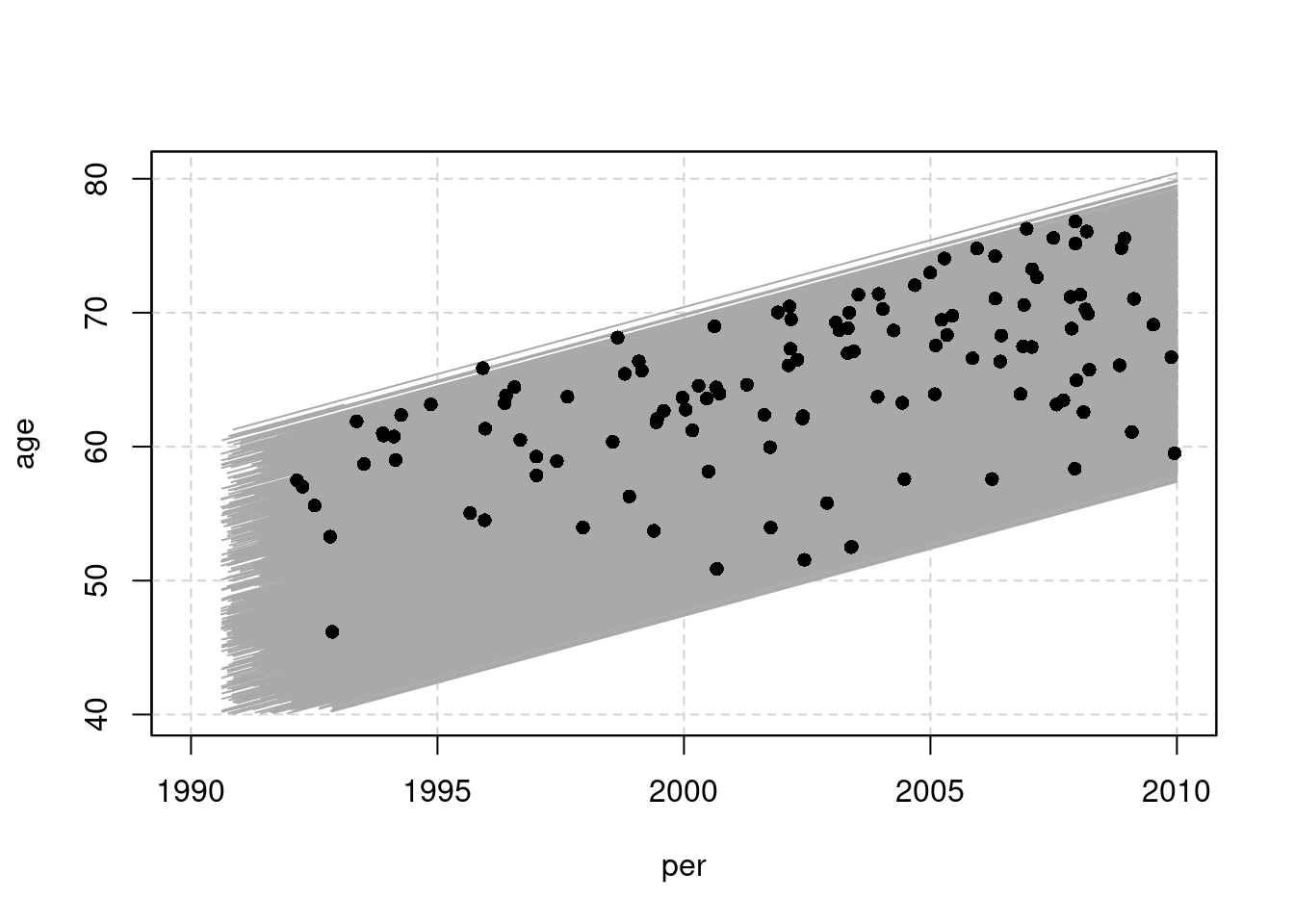

  • As age is here the main time axis, we shall graphically illustrate the study base, i.e. the follow-up lines and outcome events, only along the age scale, being ordered by age at exit. Vertical lines at those ages when new coronary deaths occur are drawn to identify the pertinent risk sets. For that purpose it is useful first to sort the data frame and the Lexis object jointly by age at exit & age at entry, and to give a new ID number according to that order.
oc.ord <- cbind(ID = 1:1501, oc[order(oc$agexit, oc$agentry), ])
oc.lexord <- Lexis(
  entry = list(age = agentry),
  exit = list(age = agexit),
  exit.status = chdeath,
  id = ID, data = oc.ord
)
## NOTE: entry.status has been set to 0 for all.
plot(oc.lexord, "age")
points(oc.lexord, pch = ifelse(oc.lexord$lex.Xst == 1, 16, NA))
with(
  subset(oc.lexord, lex.Xst == 1),
  abline(v = agexit, lty = 3)
)

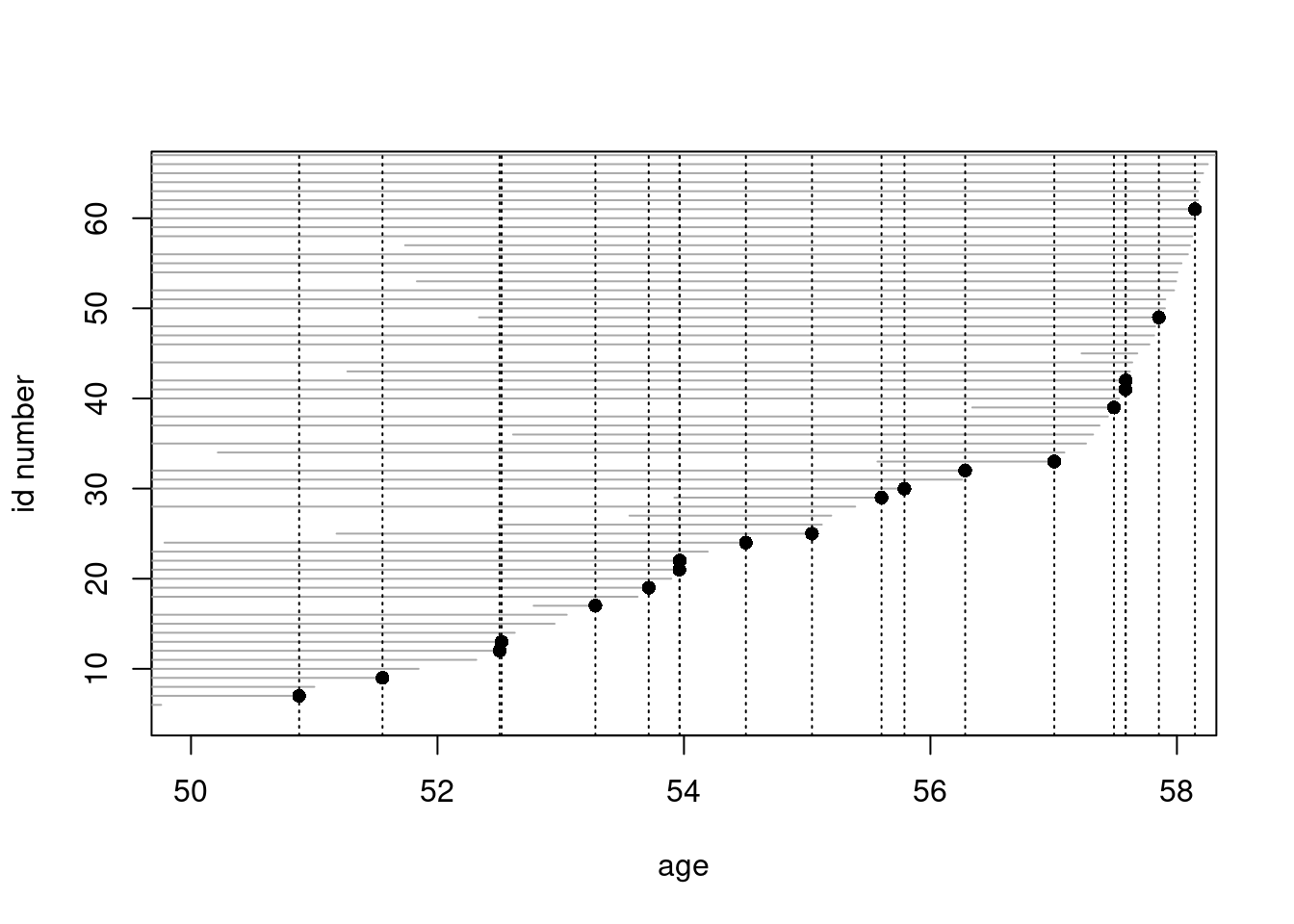
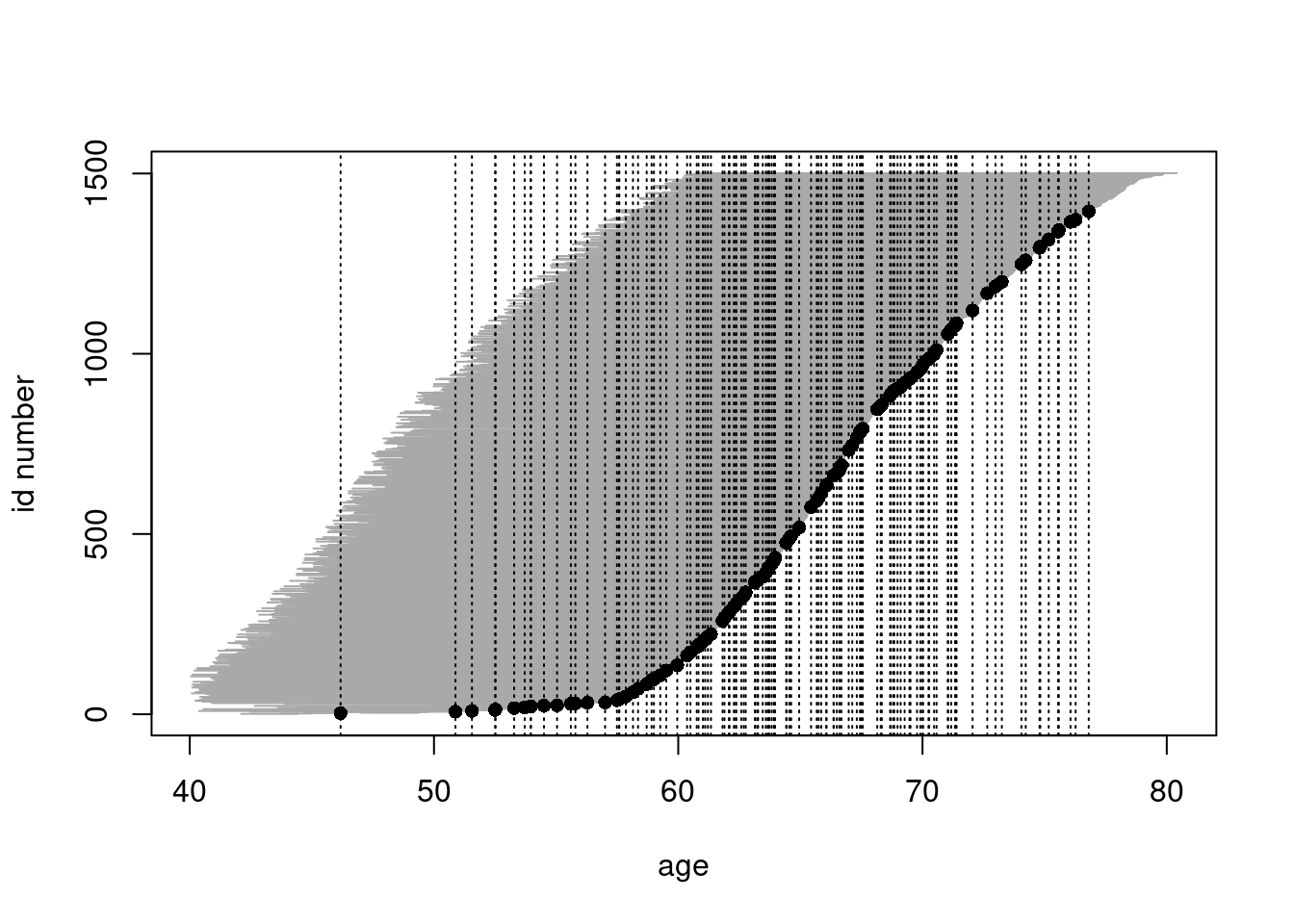- For a closer look, we now zoom the graphical illustration of the risk sets into event times occurring between 50 to 58 years. – Copy the last four lines from the previous item and add arguments xlim and ylim to the call of plot().

plot(oc.lexord, "age", xlim = c(50, 58), ylim = c(5, 65))
points(
  oc.lexord, "age", pch = ifelse(oc.lexord$lex.Xst == 1, 16, NA)
)
with(
  subset(oc.lexord, lex.Xst == 1),
  abline(v = agexit, lty = 3)
)

13.2 Nested case-control study

We shall now employ the strategy of risk-set sampling or time-matched sampling of controls, i.e. we are conducting a nested case-control study within the cohort.

  • The risk sets are defined according to the age at diagnosis of the case. Further matching is applied for age at entry by 1-year agebands. For this purpose we first generate a categorical variable agen2 for age at entry
oc.lex$agen2 <- cut(oc.lex$agentry, br = seq(40, 62, 1))

Matched sampling from risk sets may be carried out using function ccwc() found in the Epi package. Its main arguments are the times of entry and exit which specify the time at risk along the main time scale (here age), and the outcome variable to be given in the fail argument. The number of controls per case is set to be two, and the additional matching factor is given.

  • After setting the RNG seed (with your own number), make a call of this function and see the structure of the resulting data frame cactrl containing the cases and the chosen individual controls.
set.seed(98623)
cactrl <-
  ccwc(
    entry = agentry, exit = agexit, fail = chdeath,
    controls = 2, match = agen2,
    include = list(id, agentry),
    data = oc.lex, silent = FALSE
  )
## 
## Sampling risk sets: ........................................................................................................................
str(cactrl)
## 'data.frame':    360 obs. of  7 variables:
##  $ Set    : num  1 1 1 2 2 2 3 3 3 4 ...
##  $ Map    : num  8 1423 1 95 381 ...
##  $ Time   : num  63.9 63.9 63.9 66.7 66.7 ...
##  $ Fail   : num  1 0 0 1 0 0 1 0 0 1 ...
##  $ agen2  : Factor w/ 22 levels "(40,41]","(41,42]",..: 8 8 8 8 8 8 8 8 8 8 ...
##  $ id     : int  8 1423 1 95 381 106 115 44 1343 504 ...
##  $ agentry: num  47.7 47.9 47.5 47.5 48 ...

Check the meaning of the four first columns of the case-control data frame from the help page of function ccwc().

  • Now we shall start collecting data on the risk factors for the cases and their matched controls, including determination of the total cholesterol levels from the frozen sera! The storehouse of the risk factor measurements for the whole cohort is file occoh-Xdata.txt. It contains values of the following variables.
Variable Description
id identification number, the same as in occoh.txt
smok cigarette smoking with categories; 1: never, 2: former, 3: 1-14/d, 4: 15+/d
sbp systolic blood pressure (mmHg)
tchol total cholesterol level (mmol/l) 
ocX <- 
  read.table(
    paste(url, "occoh-Xdata.txt", sep = "/"), header = TRUE
  )
str(ocX)
## 'data.frame':    1501 obs. of  6 variables:
##  $ id   : int  1 2 3 4 5 6 7 8 9 10 ...
##  $ birth: chr  "1943-02-19" "1934-07-06" "1939-03-05" "1939-07-03" ...
##  $ entry: chr  "1990-08-14" "1990-08-14" "1990-08-14" "1990-08-14" ...
##  $ smok : int  4 3 3 1 2 2 1 2 1 1 ...
##  $ sbp  : int  130 128 157 102 138 119 155 154 164 124 ...
##  $ tchol: num  7.56 6.55 8.13 5.93 7.92 5.9 7.28 7.43 5.34 6.24 ...
  • In the next step we collect the values of the risk factors for our cases and controls by merging the case-control data frame and the storehouse file. In this operation we utilize function merge() to select columns of two data frames: cactrl (all columns) and ocX (four columns) and to merge these into a single file (see exercise 1.1, subsection 1.1.8, where merge() was introduced). The id variable in both files is used as the key to link each individual case or control with his own data on risk factors.
oc.ncc <- merge(cactrl, ocX[, c("id", "smok", "tchol", "sbp")],
  by = "id"
)
str(oc.ncc)
## 'data.frame':    360 obs. of  10 variables:
##  $ id     : int  1 8 10 12 14 28 37 41 41 42 ...
##  $ Set    : num  1 1 77 9 44 50 5 5 7 9 ...
##  $ Map    : num  1 8 10 12 14 28 37 41 41 42 ...
##  $ Time   : num  63.9 63.9 73 70.3 75.2 ...
##  $ Fail   : num  0 1 0 0 0 0 0 1 0 1 ...
##  $ agen2  : Factor w/ 22 levels "(40,41]","(41,42]",..: 8 8 20 17 19 19 1 1 1 17 ...
##  $ agentry: num  47.5 47.7 59.5 56.1 58.7 ...
##  $ smok   : int  4 2 1 2 4 1 3 4 4 2 ...
##  $ tchol  : num  7.56 7.43 6.24 5 3.73 4.56 5.15 6.09 6.09 5.41 ...
##  $ sbp    : int  130 154 124 148 165 230 116 125 125 156 ...
  • We shall treat smoking as categorical and total cholesterol and systolic blood pressure as quantitative risk factors, but the values of the latter will be divided by 10 to get more interpretable effect estimates.
Variable Description
cholgrp cholesterol class; 1: <5, 2: 5-<6.5, 3: >=6.5
sbpgrp blood pressure class; 1: <130, 2: 130-<150, 3: 150-<170, 4: >=170

Convert the smoking variable into a factor.

oc.ncc$smok <- factor(oc.ncc$smok,
  labels = c("never", "ex", "1-14/d", ">14/d")
)
  • It is useful to start the analysis of case-control data by simple tabulations by the categorized risk factors. Crude estimates of the rate ratios associated with them, in which matching is ignored, can be obtained as follows. We shall focus on smoking
stat.table(
  index = list(smok, Fail),
  contents = list(count(), percent(smok)),
  margins = TRUE, 
  data = oc.ncc
)
##  --------------------------------- 
##          ----------Fail----------- 
##  smok           0       1   Total  
##  --------------------------------- 
##  never         85      31     116  
##              35.4    25.8    32.2  
##                                    
##  ex            61      19      80  
##              25.4    15.8    22.2  
##                                    
##  1-14/d        54      42      96  
##              22.5    35.0    26.7  
##                                    
##  >14/d         40      28      68  
##              16.7    23.3    18.9  
##                                    
##                                    
##  Total        240     120     360  
##             100.0   100.0   100.0  
##  ---------------------------------
smok.crncc <- glm(Fail ~ smok, family = binomial, data = oc.ncc)
round(ci.exp(smok.crncc), 3)
##             exp(Est.)  2.5% 97.5%
## (Intercept)     0.365 0.242 0.550
## smokex          0.854 0.442 1.651
## smok1-14/d      2.133 1.199 3.794
## smok>14/d       1.919 1.018 3.619
  • A proper analysis takes into account matching that was employed in the selection of controls for each case from the pertinent risk set, further restricted to subjects who were about the same age at entry as the case was. Also, adjustment for the other risk factors is desirable. In this analysis function clogit() in survival package is utilized. It is in fact a wrapper of function coxph().
m.clogit <- clogit(Fail ~ smok + I(sbp / 10) + tchol +
  strata(Set), data = oc.ncc)
summary(m.clogit)
## Call:
## coxph(formula = Surv(rep(1, 360L), Fail) ~ smok + I(sbp/10) + 
##     tchol + strata(Set), data = oc.ncc, method = "exact")
## 
##   n= 360, number of events= 120 
## 
##                coef exp(coef) se(coef)      z Pr(>|z|)    
## smokex     -0.22100   0.80172  0.35085 -0.630  0.52877    
## smok1-14/d  0.59186   1.80734  0.29894  1.980  0.04772 *  
## smok>14/d   0.56616   1.76149  0.33326  1.699  0.08935 .  
## I(sbp/10)   0.11171   1.11818  0.05453  2.049  0.04050 *  
## tchol       0.40091   1.49319  0.11142  3.598  0.00032 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##            exp(coef) exp(-coef) lower .95 upper .95
## smokex        0.8017     1.2473    0.4031     1.595
## smok1-14/d    1.8073     0.5533    1.0060     3.247
## smok>14/d     1.7615     0.5677    0.9167     3.385
## I(sbp/10)     1.1182     0.8943    1.0048     1.244
## tchol         1.4932     0.6697    1.2003     1.858
## 
## Concordance= 0.679  (se = 0.046 )
## Likelihood ratio test= 28.81  on 5 df,   p=3e-05
## Wald test            = 24.31  on 5 df,   p=2e-04
## Score (logrank) test = 27.31  on 5 df,   p=5e-05
round(ci.exp(m.clogit), 3)
##            exp(Est.)  2.5% 97.5%
## smokex         0.802 0.403 1.595
## smok1-14/d     1.807 1.006 3.247
## smok>14/d      1.761 0.917 3.385
## I(sbp/10)      1.118 1.005 1.244
## tchol          1.493 1.200 1.858

Compare these with the crude estimates obtained above.

13.3 Case-cohort study

Now we start applying the second major outcome-selective sampling strategy for collecting exposure data from a big study population

  • The subcohort is selected as a
    simple random sample (\(n=260\)) from the whole cohort. The id-numbers of the individuals that are selected will be stored in vector subcids, and subcind is an indicator for inclusion to the subcohort.
N <- 1501
n <- 260
set.seed(15792)
subcids <- sample(N, n)
oc.lexord$subcind <- 1 * (oc.lexord$id %in% subcids)
  • We form the data frame oc.cc to be used in the subsequent analysis selecting the union of the subcohort members and the case group from the data frame of the full cohort. After that we collect the data of the risk factors from the data storehouse for the subjects in the case-cohort data
oc.cc <- subset(oc.lexord, subcind == 1 | chdeath == 1)
oc.cc <- merge(oc.cc, ocX[, c("id", "smok", "tchol", "sbp")],
  by = "id"
)
str(oc.cc)
## Classes 'Lexis' and 'data.frame':    362 obs. of  21 variables:
##  $ id     : int  8 10 34 40 41 42 43 45 51 62 ...
##  $ age    : num  47.7 59.5 51.9 45.2 40.2 ...
##  $ lex.dur: num  16.21 19.38 19.36 4.59 19.32 ...
##  $ lex.Cst: num  0 0 0 0 0 0 0 0 0 0 ...
##  $ lex.Xst: int  1 0 0 0 1 1 1 0 1 1 ...
##  $ lex.id : int  430 1483 1074 6 121 987 746 486 1056 663 ...
##  $ ID     : int  430 1483 1074 6 121 987 746 486 1056 663 ...
##  $ birth  : chr  "1942-11-24" "1931-03-01" "1938-09-14" "1945-06-22" ...
##  $ entry  : chr  "1990-08-15" "1990-08-15" "1990-08-20" "1990-08-21" ...
##  $ exit   : chr  "2006-10-30" "2009-12-31" "2009-12-31" "1995-03-26" ...
##  $ death  : int  1 0 0 1 1 1 1 0 1 1 ...
##  $ chdeath: int  1 0 0 0 1 1 1 0 1 1 ...
##  $ ybirth : num  1943 1931 1939 1945 1950 ...
##  $ yentry : num  1991 1991 1991 1991 1991 ...
##  $ yexit  : num  2007 2010 2010 1995 2010 ...
##  $ agentry: num  47.7 59.5 51.9 45.2 40.2 ...
##  $ agexit : num  63.9 78.8 71.3 49.8 59.5 ...
##  $ subcind: num  0 1 1 1 0 0 0 1 1 0 ...
##  $ smok   : int  2 1 1 4 4 2 3 2 1 2 ...
##  $ tchol  : num  7.43 6.24 5.8 5.88 6.09 5.41 5.72 5.98 7.12 5.57 ...
##  $ sbp    : int  154 124 113 141 125 156 128 115 137 173 ...
##  - attr(*, "breaks")=List of 1
##   ..$ age: NULL
##  - attr(*, "time.scales")= chr "age"
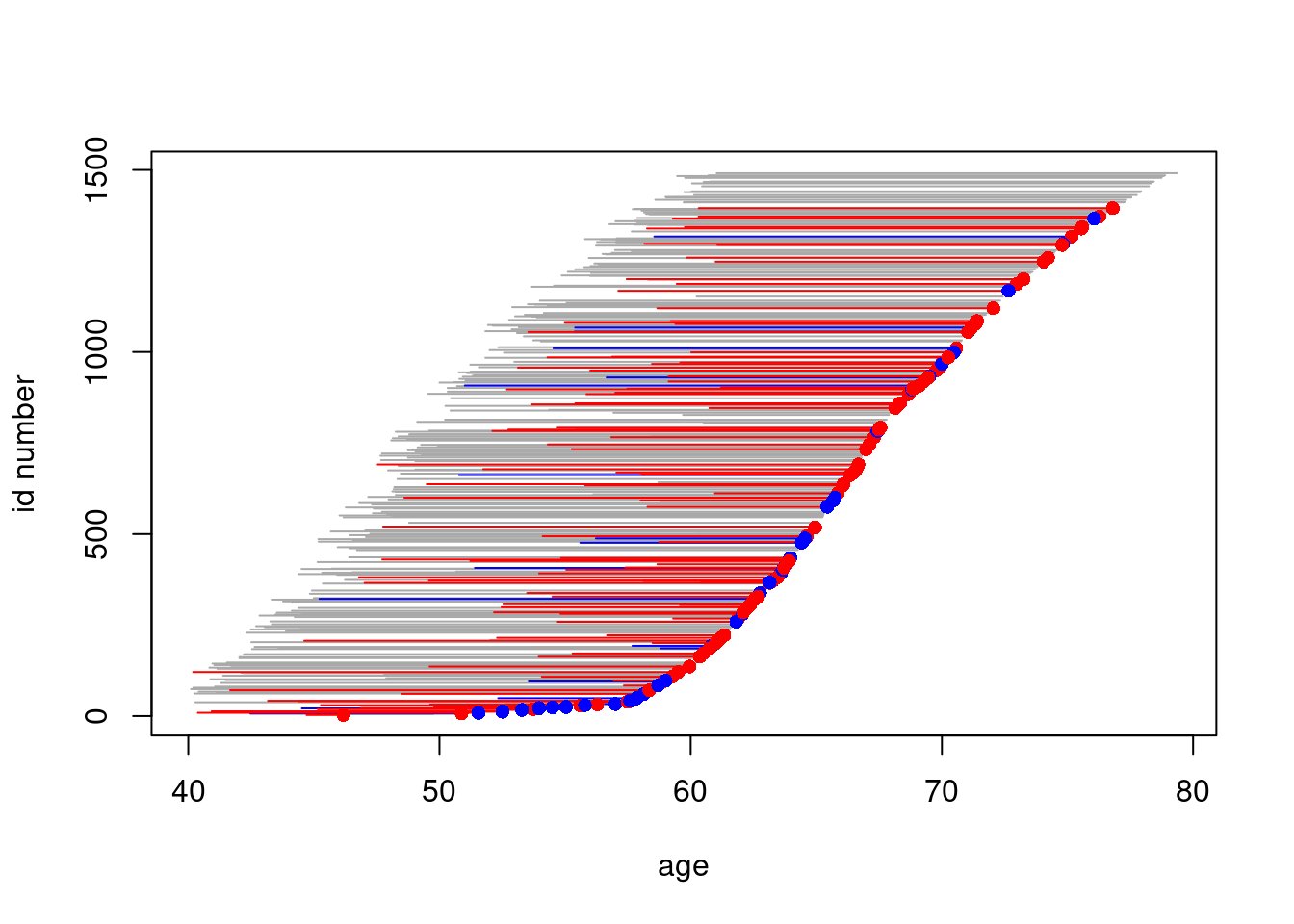
##  - attr(*, "time.since")= chr ""
  • We shall now create a graphical illustration of the lifelines contained in the case-cohort data. Lines for the subcohort non-cases are grey without bullet at exit, those for subcohort cases are blue with blue bullet at exit, and for cases outside the subcohort the lines are red and dotted with red bullets at exit.
plot(subset(oc.cc, chdeath == 0), "age")
lines(subset(oc.cc, chdeath == 1 & subcind == 1), col = "blue")
lines(subset(oc.cc, chdeath == 1 & subcind == 0), col = "red")
points(subset(oc.cc, chdeath == 1),
  pch = 16,
  col = c("blue", "red")[oc.cc$subcind + 1]
)

  • Define the categorical smoking variable again.
oc.cc$smok <- factor(oc.cc$smok,
  labels = c("never", "ex", "1-14/d", ">14/d")
)

A crude estimate of the hazard ratio for the various smoking categories \(k\) vs. non-smokers (\(k=1\)) can be obtained by tabulating cases \((D_k)\) and person-years (\(y_k\)) in the subcohort by smoking and then computing the relevant exposure odds ratio for each category: \[ \text{HR}_k ^{\text{crude}} = \frac{D_k/D_1}{y_k/y_1} \]

sm.cc <- stat.table(
  index = smok,
  contents = list(Cases = sum(lex.Xst), Pyrs = sum(lex.dur)),
  margins = TRUE, 
  data = oc.cc
)
print(sm.cc, digits = c(sum = 0, ratio = 1))
##  ------------------------- 
##  smok       Cases    Pyrs  
##  ------------------------- 
##  never         31    2071  
##  ex            19    1174  
##  1-14/d        42    1399  
##  >14/d         28     846  
##                            
##  Total        120    5489  
##  -------------------------
HRcc <- 
  (sm.cc[1, -5] / sm.cc[1, 1]) / (sm.cc[2, -5] / sm.cc[2, 1])
round(HRcc, 3)
##  never     ex 1-14/d  >14/d 
##  1.000  1.081  2.006  2.211

Do these estimates resemble those obtained from nested case-control data?

  • To estimate the rate ratios associated with smoking and adjusted for the other risk factors we now fit the pertinent Cox model applying the method of weighted partial likelihood as presented by Ling & Ying (1993) and Barlow (1994). This analysis can be done using function cch() in package survival with method = "LinYing"
oc.cc$survobj <- with(oc.cc, Surv(agentry, agexit, chdeath))
cch.LY <- cch(survobj ~ smok + I(sbp / 10) + tchol,
  stratum = NULL,
  subcoh = ~subcind, id = ~id, cohort.size = N, data = oc.cc,
  method = "LinYing"
)
summary(cch.LY)
## Case-cohort analysis,x$method, LinYing 
##  with subcohort of 260 from cohort of 1501 
## 
## Call: cch(formula = survobj ~ smok + I(sbp/10) + tchol, data = oc.cc, 
##     subcoh = ~subcind, id = ~id, stratum = NULL, cohort.size = N, 
##     method = "LinYing")
## 
## Coefficients:
##              Coef    HR  (95%   CI)     p
## smokex     -0.096 0.909 0.457 1.806 0.785
## smok1-14/d  0.769 2.157 1.180 3.943 0.012
## smok>14/d   1.085 2.959 1.532 5.718 0.001
## I(sbp/10)   0.218 1.244 1.119 1.383 0.000
## tchol       0.350 1.419 1.152 1.748 0.001

13.4 Full cohort analysis and comparisons

Finally, suppose the investigators after all could afford to collect the data on risk factors from the storehouse for the whole cohort.

  • Let us form the data frame corresponding to the full cohort design and convert again smoking to be categorical.
oc.full <- merge(oc.lex, ocX[, c("id", "smok", "tchol", "sbp")],
  by.x = "id", by.y = "id"
)
oc.full$smok <- factor(oc.full$smok,
  labels = c("never", "ex", "1-14/d", ">14/d")
)

Juts for comparison with the corresponding analysis in case-cohort data perform a similar crude estimation of hazard ratios associated with smoking.

sm.coh <- stat.table(
  index = smok,
  contents = list(Cases = sum(lex.Xst), Pyrs = sum(lex.dur)),
  margins = TRUE, 
  data = oc.full
)
print(sm.coh, digits = c(sum = 0, ratio = 1))
##  ------------------------- 
##  smok       Cases    Pyrs  
##  ------------------------- 
##  never         31   10363  
##  ex            19    4879  
##  1-14/d        42    6246  
##  >14/d         28    3793  
##                            
##  Total        120   25281  
##  -------------------------
HRcoh <- 
  (sm.coh[1, -5] / sm.coh[1, 1]) / (sm.coh[2, -5] / sm.coh[2, 1])
round(HRcoh, 3)
##  never     ex 1-14/d  >14/d 
##  1.000  1.302  2.248  2.468
  • Fit now the ordinary Cox model to the full cohort. There is no need to employ extra tricks upon the ordinary coxph() fit.
cox.coh <- coxph(Surv(agentry, agexit, chdeath) ~
  smok + I(sbp / 10) + tchol, data = oc.full)
summary(cox.coh)
## Call:
## coxph(formula = Surv(agentry, agexit, chdeath) ~ smok + I(sbp/10) + 
##     tchol, data = oc.full)
## 
##   n= 1501, number of events= 120 
## 
##               coef exp(coef) se(coef)     z Pr(>|z|)    
## smokex     0.10955   1.11577  0.29240 0.375 0.707922    
## smok1-14/d 0.72567   2.06612  0.23704 3.061 0.002203 ** 
## smok>14/d  0.95054   2.58711  0.26198 3.628 0.000285 ***
## I(sbp/10)  0.14372   1.15456  0.04096 3.509 0.000450 ***
## tchol      0.26517   1.30366  0.07089 3.740 0.000184 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##            exp(coef) exp(-coef) lower .95 upper .95
## smokex         1.116     0.8962     0.629     1.979
## smok1-14/d     2.066     0.4840     1.298     3.288
## smok>14/d      2.587     0.3865     1.548     4.323
## I(sbp/10)      1.155     0.8661     1.065     1.251
## tchol          1.304     0.7671     1.135     1.498
## 
## Concordance= 0.681  (se = 0.026 )
## Likelihood ratio test= 41.16  on 5 df,   p=9e-08
## Wald test            = 42.05  on 5 df,   p=6e-08
## Score (logrank) test = 43.29  on 5 df,   p=3e-08
  • Lastly, a comparison of the point estimates and standard errors between the different designs, including variants of analysis for the case-cohort design, can be performed.
betas <- cbind(coef(cox.coh), coef(m.clogit), coef(cch.LY))
colnames(betas) <- c("coh", "ncc", "cch.LY")
round(betas, 3)
##              coh    ncc cch.LY
## smokex     0.110 -0.221 -0.096
## smok1-14/d 0.726  0.592  0.769
## smok>14/d  0.951  0.566  1.085
## I(sbp/10)  0.144  0.112  0.218
## tchol      0.265  0.401  0.350
SEs <- cbind(
  sqrt(diag(cox.coh$var)),
  sqrt(diag(m.clogit$var)),
  sqrt(diag(cch.LY$var))
)
colnames(SEs) <- colnames(betas)
round(SEs, 3)
##              coh   ncc cch.LY
## smokex     0.292 0.351  0.350
## smok1-14/d 0.237 0.299  0.308
## smok>14/d  0.262 0.333  0.336
## I(sbp/10)  0.041 0.055  0.054
## tchol      0.071 0.111  0.106

You will notice that the point estimates of the coefficients obtained from the full cohort, nested case-control, and case-cohort analyses, respectively, are somewhat variable. However,
the standard errors from the NCC and CC analyses should be quite similar when the numbers of cases and non-cases are similar.

13.5 Further exercises and homework

  • If you have time, you could run both the NCC study and CC study again but now with a larger control group or subcohort; for example 4 controls per case in NCC and \(n=520\) as the subcohort size in CC. Remember resetting the seed first. Pay attention in the results to how much closer will be the point estimates and the proper SEs to those obtained from the full cohort design.

  • Instead of simple linear terms for sbp and tchol you could try to fit spline models to describe their effects.

  • A popular alternative to weighted partial likelihood in the analysis of case-cohort data is the pseudo-likelihood method (Prentice 1986), which is based on late entry to follow-up of the case subjects not belonging to the subcohort. The way to do this is provided by function cch() which you can apply directly to the case-cohort data oc.cc as before but now with method = "Prentice". – Try this and compare the results with those obtained by weighted partial likelihood in model cch.LY.

  • Yet another computational solution for maximizing weighted partial likelihood is provided by a combination of functions twophase() and svycoxph() of the survey package. The approach is illustrated with an example in a vignette Two-phase designs in epidemiology by Thomas Lumley (see http://cran.r-project.org/web/packages/survey/vignettes/epi.pdf). – You can try this at home and check that you would obtain similar results as with model cch.LY.