Chapter 15 Time-dependent variables and multiple states

The following practical exercise is based on the data from paper:

P Hovind, L Tarnow, P Rossing, B Carstensen, and HH Parving: Improved survival in patients obtaining remission of nephrotic range albuminuria in diabetic nephropathy. Kidney Int, 66(3):1180–1186, Sept 2004.

You can find a .pdf-version of the paper here: http://BendixCarstensen.com/AdvCoh/papers/Hovind.2004.pdf

15.1 The renal failure dataset

The dataset renal.dta contains data on follow up of 125 patients from Steno Diabetes Center. They enter the study when they are diagnosed with nephrotic range albuminuria (NRA). This is a condition where the levels of albumin in the urine is exceeds a certain level as a sign of kidney disease. The levels may however drop as a consequence of treatment, this is called remission. Patients exit the study at death or kidney failure (dialysis or transplant).

Variable Description
id Patient id
sex 1=male, 2=female
dob Date of birth
doe Date of entry into the study (2.5 years after NRA)
dor Date of remission. Missing if no remission has occurred
dox Date of exit from study
event Exit status: 1,2,3=event (death, ESRD), 0=censored

  1. The dataset is in Stata-format, so you must read the dataset using read.dta from the foreign package (which is part of the standard R-distribution). At the same time, convert sex to a proper factor. Choose where to read the dataset.

    library(Epi)
library(survival)
library(mgcv)
    Loading required package: nlme
    This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
    library(foreign)
# renal <- read.dta(
#  "https://raw.githubusercontent.com/SPE-R/SPE/master/pracs/data/renal.dta")
renal <- read.dta("http://BendixCarstensen.com/SPE/data/renal.dta")
renal$sex <- factor(renal$sex, labels = c("M", "F"))
head(renal)

  2. Use the Lexis function to declare the data as survival data with age, calendar time and time since entry into the study as timescales. Label any event \(>0\) as ESRD, i.e. renal death (death of kidney (transplant or dialysis), or person). Note that you must make sure that the alive state (here NRA) is the first, as Lexis assumes that everyone starts in this state (unless of course entry.status is specified):

    Lr <- Lexis(entry = list(per = doe,
                         age = doe - dob,
                         tfi = 0),
             exit = list(per = dox),
      exit.status = factor(event > 0, labels = c("NRA", "ESRD")),
             data = renal)
    NOTE: entry.status has been set to "NRA" for all.
    str(Lr)
    Classes 'Lexis' and 'data.frame':   125 obs. of  14 variables:
 $ per    : num  1996 1990 1988 1995 1988 ...
 $ age    : num  28.1 30.2 25.8 44.5 26.6 ...
 $ tfi    : num  0 0 0 0 0 0 0 0 0 0 ...
 $ lex.dur: num  1.08 6.6 5.39 8.75 16.07 ...
 $ lex.Cst: Factor w/ 2 levels "NRA","ESRD": 1 1 1 1 1 1 1 1 1 1 ...
 $ lex.Xst: Factor w/ 2 levels "NRA","ESRD": 2 2 2 1 1 2 2 1 2 1 ...
 $ lex.id : int  1 2 3 4 5 6 7 8 9 10 ...
 $ id     : num  17 26 27 33 42 46 47 55 62 64 ...
 $ sex    : Factor w/ 2 levels "M","F": 1 2 2 1 2 2 1 1 2 1 ...
 $ dob    : num  1968 1959 1962 1951 1961 ...
 $ doe    : num  1996 1990 1988 1995 1988 ...
 $ dor    : num  NA 1990 NA 1996 1997 ...
 $ dox    : num  1997 1996 1993 2004 2004 ...
 $ event  : num  2 1 3 0 0 2 1 0 2 0 ...
 - attr(*, "time.scales")= chr [1:3] "per" "age" "tfi"
 - attr(*, "time.since")= chr [1:3] "" "" ""
 - attr(*, "breaks")=List of 3
  ..$ per: NULL
  ..$ age: NULL
  ..$ tfi: NULL
    summary(Lr)
    
Transitions:
     To
From  NRA ESRD  Records:  Events: Risk time:  Persons:
  NRA  48   77       125       77    1084.67       125

    Make sure you know what the variables in Lr stand for.

  3. Visualize the follow-up in a Lexis-diagram, by using the plot method for Lexis objects.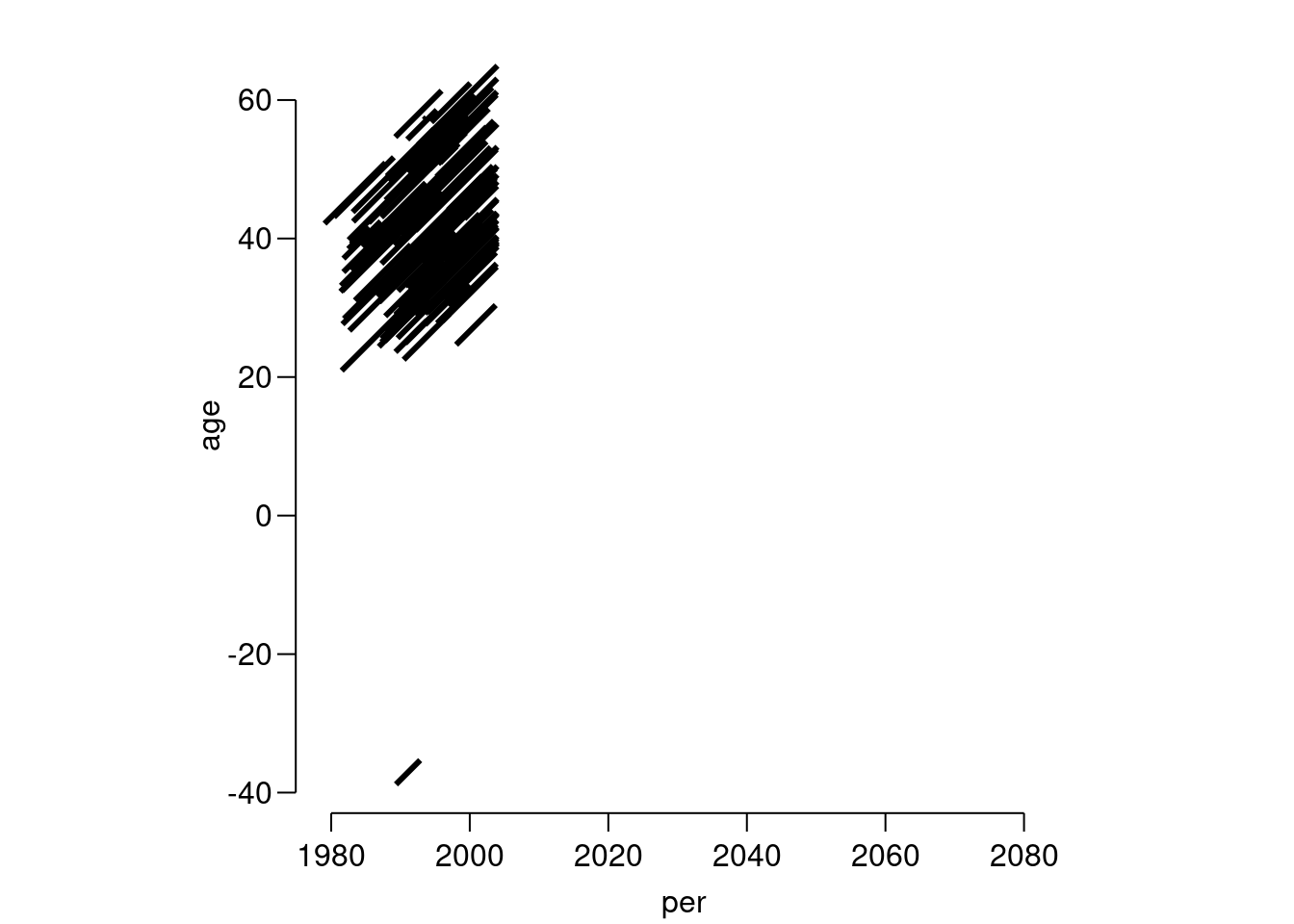

    plot(Lr, col = "black", lwd = 3)

    subset(Lr, age < 0)
     lex.id     per    age tfi lex.dur lex.Cst lex.Xst  id sex      dob      doe dor      dox
     88 1989.34 -38.81   0     3.5     NRA    ESRD 586   M 2028.155 1989.343  NA 1992.839
 event
     1

    What is wrong here? List the data for the person with negative entry age.

  4. Correct the data and make a new plot, for example by:

    Lr <- transform(Lr, age = ifelse(dob > 2000, age + 100, age),
                    dob = ifelse(dob > 2000, dob - 100, dob))
subset(Lr, id == 586)
     lex.id     per   age tfi lex.dur lex.Cst lex.Xst  id sex      dob      doe dor      dox
     88 1989.34 61.19   0     3.5     NRA    ESRD 586   M 1928.155 1989.343  NA 1992.839
 event
     1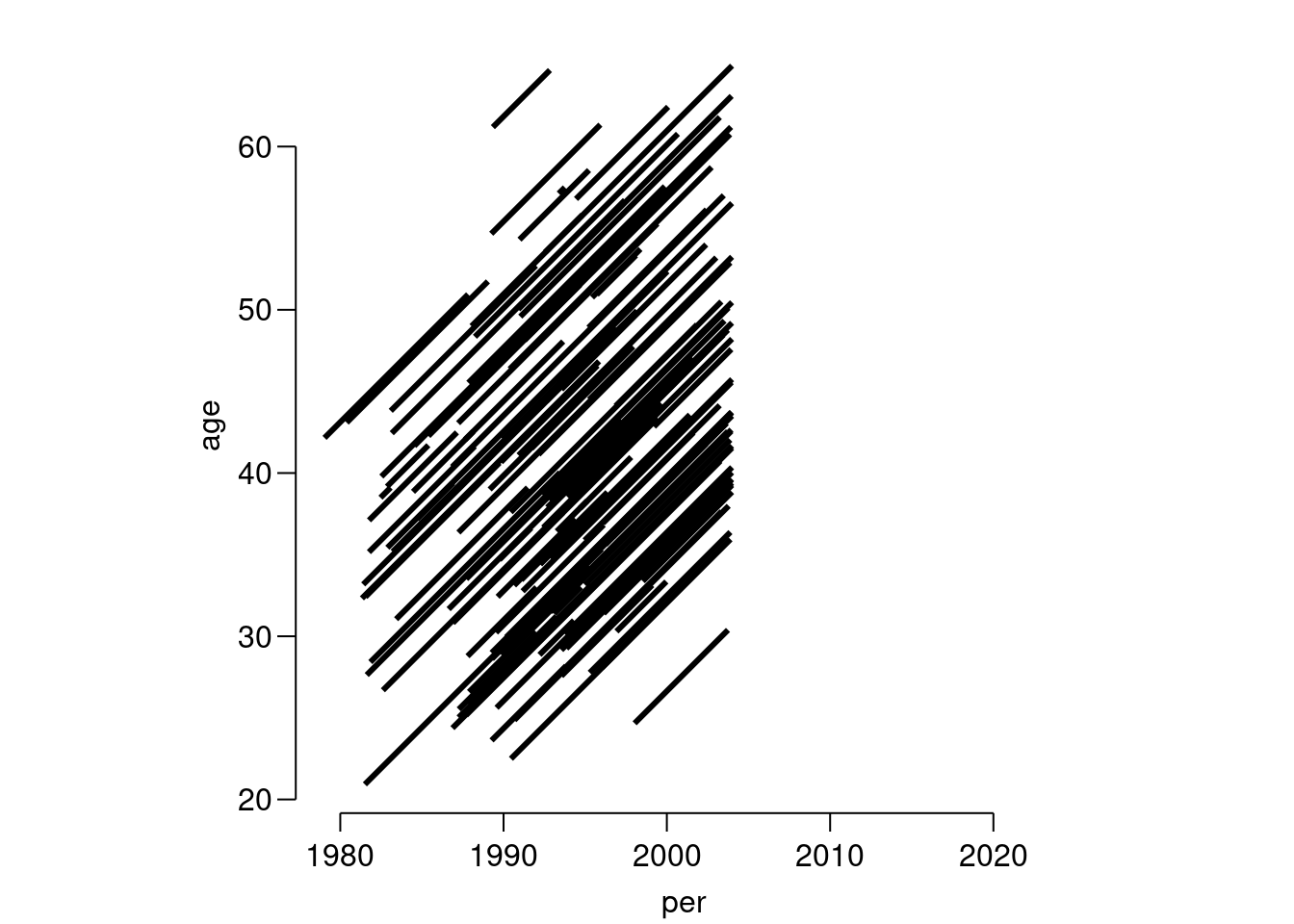
    plot(Lr, col = "black", lwd = 3)

  5. Now make a Cox-regression analysis of ESRD occurrence with the variables sex and age at entry into the study, using time since entry to the study as time scale.

    mc <- coxph(Surv(lex.dur, lex.Xst == "ESRD") 
            ~ I(age / 10) + sex, data = Lr)
summary(mc)
    Call:
coxph(formula = Surv(lex.dur, lex.Xst == "ESRD") ~ I(age/10) + 
    sex, data = Lr)

  n= 125, number of events= 77 

             coef exp(coef) se(coef)      z Pr(>|z|)
I(age/10)  0.5514    1.7357   0.1402  3.932 8.43e-05
sexF      -0.1817    0.8338   0.2727 -0.666    0.505

          exp(coef) exp(-coef) lower .95 upper .95
I(age/10)    1.7357     0.5761    1.3186     2.285
sexF         0.8338     1.1993    0.4886     1.423

Concordance= 0.612  (se = 0.036 )
Likelihood ratio test= 16.07  on 2 df,   p=3e-04
Wald test            = 16.38  on 2 df,   p=3e-04
Score (logrank) test = 16.77  on 2 df,   p=2e-04

    What is the hazard ratio between males and females? Between two persons who differ 10 years in age at entry?

  6. The main focus of the paper was to assess whether the occurrence of remission (return to a lower level of albumin excretion, an indication of kidney recovery) influences mortality. Remission is a time-dependent variable which is initially 0, but takes the value 1 when remission occurs. In order to handle this, each person who sees a remission must have two records:

    • One record for the time before remission, where entry is doe, exit is dor, remission is 0, and event is 0.
    • One record for the time after remission, where entry is dor, exit is dox, remission is 1, and event is 0 or 1 according to whether the person had an event at dox.

    This is accomplished using the cutLexis function on the Lexis object, where we introduce a remission state Rem. Also use split.state=TRUE to have different ESRD states according to whether a person had had remission or not prioer to ESRD. The statement to do this is:

    Lc <- cutLexis(Lr, cut = Lr$dor, # where to cut follow up
             timescale = "per",  # what timescale are we referring to
             new.state = "Rem",  # name of the new state
           split.state = TRUE)   # different states depending on previous
summary(Lc)
    
Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA  24  29   69         0       122       98     824.77       122
  Rem   0  24    0         8        32        8     259.90        32
  Sum  24  53   69         8       154      106    1084.67       125

    List the records from a few select persons (choose values for lex.id, using for example subset(Lc, lex.id %in% c(5,7,9))).

  7. Now show how the states are connected and the number of transitions between them by using boxes. This is an interactive command that requires you to click in the graph window:

    boxes(Lc)

    It has a couple of fancy arguments, try:

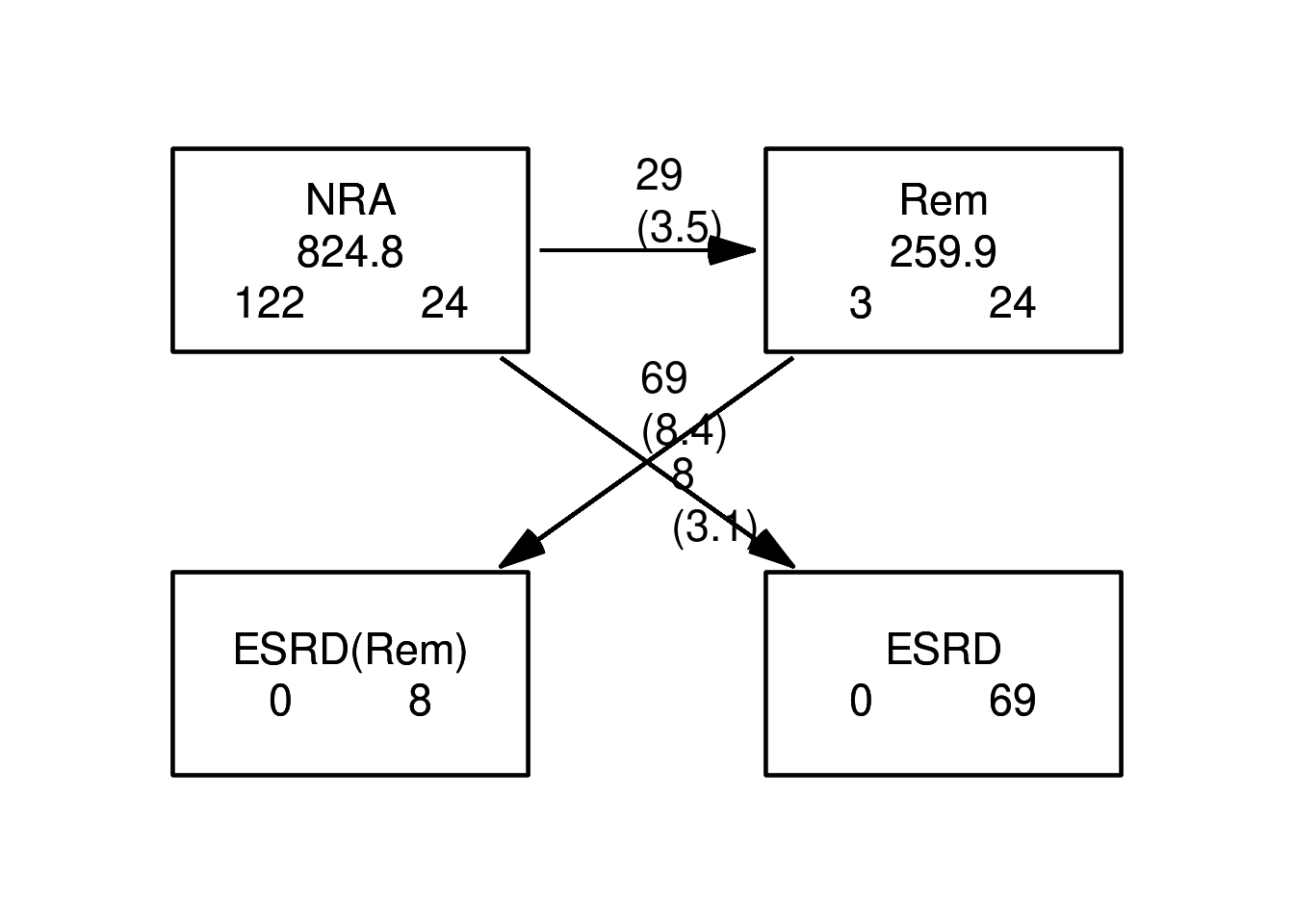
    boxes(Lc, boxpos = TRUE, scale.R = 100, show.BE = TRUE, hm = 1.5, wm = 1.5)

    You may even be tempted to read the help page for boxes.Lexis …

  8. Plot a Lexis diagram where different coloring is used for different segments of the follow-up. The plot.Lexis function draws a line for each record in the dataset, so you can index the coloring by lex.Cst and lex.Xst as appropriate — indexing by a factor corresponds to indexing by the index number of the factor levels, so you must be know which order the factor levels are in:

    levels(Lc) # names and order of states in lex.Cst and lex.Xst
    [1] "NRA"       "Rem"       "ESRD"      "ESRD(Rem)"
    par(mai = c(3, 3, 1, 1) / 4, mgp = c(3, 1, 0) / 1.6)
plot(Lc, col = c("red", "limegreen")[Lc$lex.Cst],
        xlab = "Calendar time", ylab = "Age",
         lwd = 3, grid = 0:20 * 5, las = 1,
        xlim = c(1970, 2010), ylim = c(20, 70), 
        xaxs = "i", yaxs = "i")
points(Lc, pch = c(NA, NA, 16, 16)[Lc$lex.Xst],
           col = c("red", "limegreen", "transparent", "transparent")[Lc$lex.Cst])
points(Lc, pch = c(NA, NA, 1, 1)[Lc$lex.Xst],
           col = "black", lwd = 2)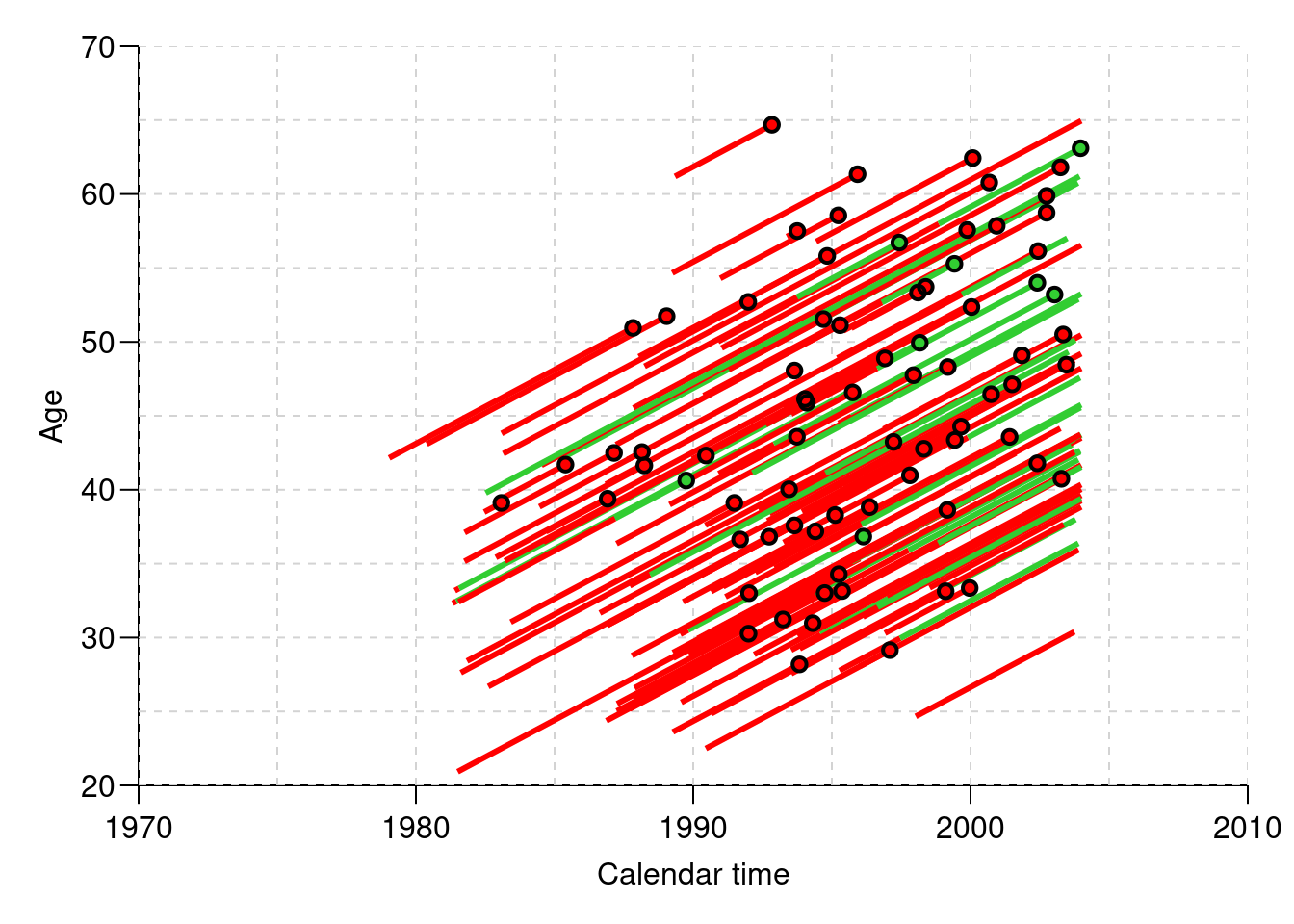

  9. Make a Cox-regression of mortality rates (i.e. endpoint ESRD or ESRD(Rem)) with sex, age at entry and remission as explanatory variables, using time since entry as timescale, and include lex.Cst as time-dependent variable, and indicate that each record represents follow-up from tfi to tfi+lex.dur. Make sure that you know why what goes where here in the call to coxph.

    (EP <- levels(Lc)[3:4])           # define EndPoint states
    [1] "ESRD"      "ESRD(Rem)"
    m1 <- coxph(Surv(tfi,             # entry time
                 tfi + lex.dur,   # exit time
                 lex.Xst %in% EP) # event
            ~ sex + I((doe - dob - 50) / 10) + # fixed covariates
              (lex.Cst == "Rem"),              # time-dependent variable
            data = Lc)
summary(m1)
    Call:
coxph(formula = Surv(tfi, tfi + lex.dur, lex.Xst %in% EP) ~ sex + 
    I((doe - dob - 50)/10) + (lex.Cst == "Rem"), data = Lc)

  n= 154, number of events= 77 

                           coef exp(coef) se(coef)      z Pr(>|z|)
sexF                   -0.05534   0.94616  0.27500 -0.201 0.840517
I((doe - dob - 50)/10)  0.52190   1.68522  0.13655  3.822 0.000132
lex.Cst == "Rem"TRUE   -1.26241   0.28297  0.38483 -3.280 0.001036

                       exp(coef) exp(-coef) lower .95 upper .95
sexF                      0.9462     1.0569    0.5519    1.6220
I((doe - dob - 50)/10)    1.6852     0.5934    1.2895    2.2024
lex.Cst == "Rem"TRUE      0.2830     3.5339    0.1331    0.6016

Concordance= 0.664  (se = 0.033 )
Likelihood ratio test= 30.31  on 3 df,   p=1e-06
Wald test            = 27.07  on 3 df,   p=6e-06
Score (logrank) test = 29.41  on 3 df,   p=2e-06

    What is the effect of of remission on the rate of ESRD?

    Splitting the follow-up time

    In order to explore the effect of remission on the rate of ESRD, we split the data further into small pieces of follow-up. To this end we use the function splitLexis. The rates can then be modeled using a Poisson-model, and the shape of the effect of the underlying rates be explored. Furthermore, we can allow effects of both time since NRA and current age. To this end we will use splines, so we need the splines and also the mgcv packages.

  10. Now split the follow-up time every month after entry, and verify that the number of events and risk time is the same as before and after the split:

    sLc <- splitLexis(Lc, "tfi", breaks = seq(0, 30, 1/12))
summary( Lc)
    
Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA  24  29   69         0       122       98     824.77       122
  Rem   0  24    0         8        32        8     259.90        32
  Sum  24  53   69         8       154      106    1084.67       125
    summary(sLc)
    
Transitions:
     To
From   NRA  Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA 9854   29   69         0      9952       98     824.77       122
  Rem    0 3139    0         8      3147        8     259.90        32
  Sum 9854 3168   69         8     13099      106    1084.67       125

  11. Now fit the Poisson-model corresponding to the Cox-model we fitted previously. The function Ns() produces a model matrix corresponding to a piece-wise cubic function, modeling the baseline hazard explicitly (think of the Ns terms as the baseline hazard that is not visible in the Cox-model). You can use the wrapper function glm.Lexis

    mp <- glm.Lexis(sLc, 
                ~ Ns(tfi, knots = c(0, 2, 5, 10)) +
                  sex + I((doe - dob - 40) / 10) + 
                  I(lex.Cst == "Rem"))
    stats::glm Poisson analysis of Lexis object sLc with log link:
Rates for transitions:
NRA->ESRD
Rem->ESRD(Rem)
    ci.exp(mp)
                                       exp(Est.)        2.5%        97.5%
(Intercept)                       0.01664432 0.003956666   0.07001685
Ns(tfi, knots = c(0, 2, 5, 10))1  5.18917655 1.949197027  13.81469029
Ns(tfi, knots = c(0, 2, 5, 10))2 34.20004199 1.764818735 662.75524463
Ns(tfi, knots = c(0, 2, 5, 10))3  4.43318269 2.179977108   9.01528219
sexF                              0.91751162 0.536258443   1.56981691
I((doe - dob - 40)/10)            1.70082390 1.300813859   2.22384004
I(lex.Cst == "Rem")TRUE           0.27927558 0.131396852   0.59358233

    How does the effects of sex change from the Cox-model?

  12. Try instead using the gam function from the mgcv package. There is convenience wrapper for this for Lexis objects as well:

    mx <- gam.Lexis(sLc,
                ~ s(tfi, k = 10) + 
                  sex + I((doe - dob - 40) / 10) + 
                  I(lex.Cst == "Rem"))
    mgcv::gam Poisson analysis of Lexis object sLc with log link:
Rates for transitions:
NRA->ESRD
Rem->ESRD(Rem)
    ci.exp(mp, subset = c("Cst", "doe", "sex"))
                            exp(Est.)      2.5%     97.5%
I(lex.Cst == "Rem")TRUE 0.2792756 0.1313969 0.5935823
I((doe - dob - 40)/10)  1.7008239 1.3008139 2.2238400
sexF                    0.9175116 0.5362584 1.5698169
    ci.exp(mx, subset = c("Cst", "doe", "sex"))
                            exp(Est.)      2.5%     97.5%
I(lex.Cst == "Rem")TRUE 0.2784659 0.1309446 0.5921838
I((doe - dob - 40)/10)  1.6992069 1.2995225 2.2218192
sexF                    0.9309945 0.5435486 1.5946150

    We see that there is virtually no difference between the two approaches in terms of the regression parameters.

  13. Extract the regression parameters from the models using ci.exp and compare with the estimates from the Cox-model:

    ci.exp(mx, subset = c("sex", "dob", "Cst"), pval = TRUE)
                            exp(Est.)      2.5%     97.5%            P
sexF                    0.9309945 0.5435486 1.5946150 0.7945394004
I((doe - dob - 40)/10)  1.6992069 1.2995225 2.2218192 0.0001066910
I(lex.Cst == "Rem")TRUE 0.2784659 0.1309446 0.5921838 0.0008970863
    ci.exp(m1)
                           exp(Est.)      2.5%    97.5%
sexF                   0.9461646 0.5519334 1.621985
I((doe - dob - 50)/10) 1.6852196 1.2895097 2.202360
lex.Cst == "Rem"TRUE   0.2829710 0.1330996 0.601599
    round(ci.exp(mp, subset = c("sex", "dob", "Cst")) / ci.exp(m1), 2)
                            exp(Est.) 2.5% 97.5%
sexF                         0.97 0.97  0.97
I((doe - dob - 40)/10)       1.01 1.01  1.01
I(lex.Cst == "Rem")TRUE      0.99 0.99  0.99

    How large are the differences in estimated regression parameters?

  14. The model has the same assumptions as the Cox-model about proportionality of rates, but there is an additional assumption that the hazard is a smooth function of time since entry. It seems to be a sensible assumption (well, restriction) to put on the rates that they vary smoothly by time. No such restriction is made in the Cox model. The gam model optimizes the shape of the smoother by general cross-validation. Try to look at the shape of the estimated effect of tfi: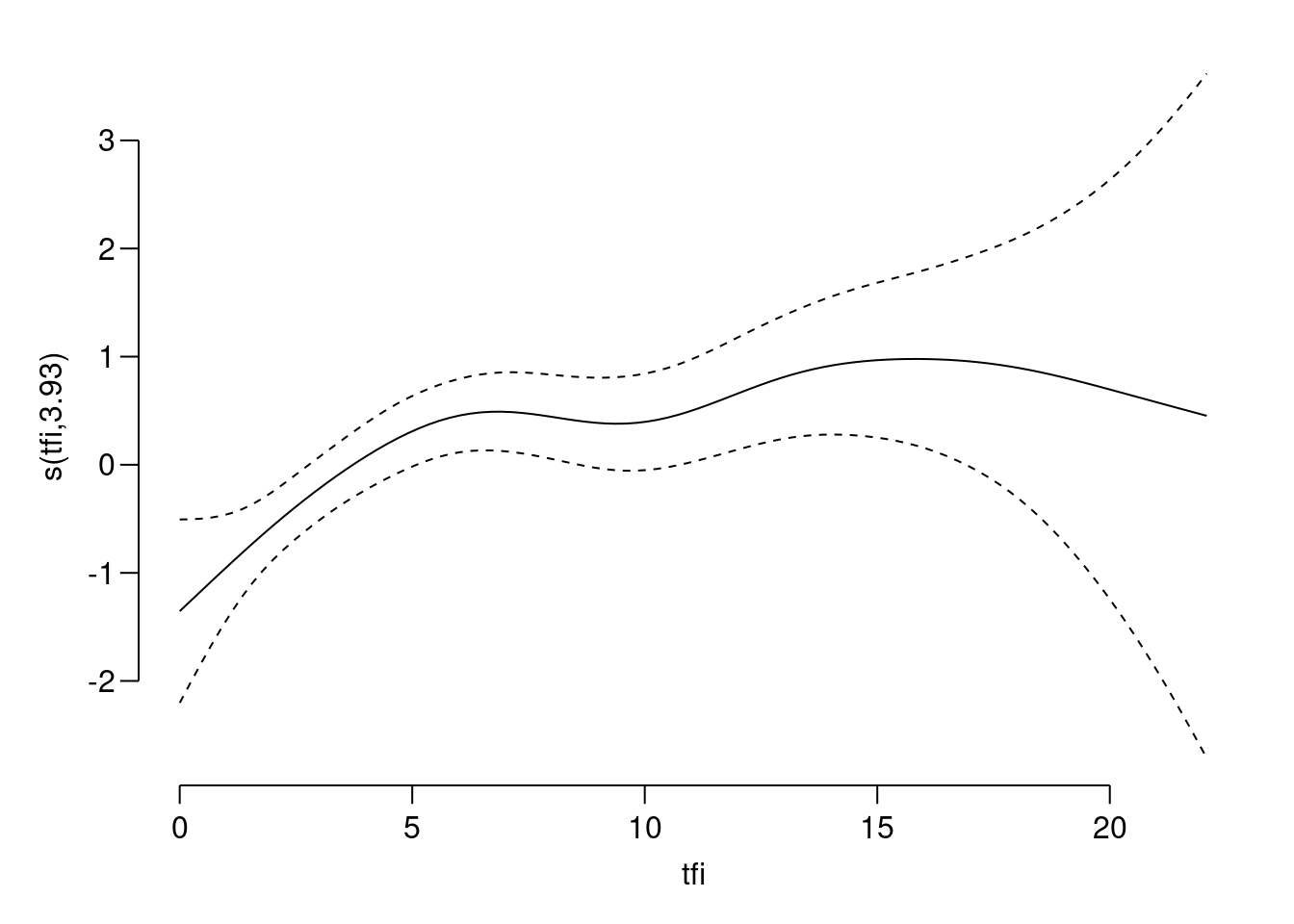

    plot(mx)

    Is this a useful plot?

  15. However, plot (well, plot.gam) does not give you the absolute level of the underlying rates because it bypasses the intercept. So in order to predict the rates as a function of tfi and the covariates, we set up a prediction data frame. Note that age in the model specification is entered as doe-dob, hence the prediction data frame must have these two variables and not the age, but it is only the difference that matters for the prediction:

    nd <- data.frame(tfi = seq(0, 20, 0.1),
                 sex = "M",
                 doe = 1990,
                 dob = 1940,
             lex.Cst = "NRA")
str(nd)
    'data.frame':   201 obs. of  5 variables:
 $ tfi    : num  0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 ...
 $ sex    : chr  "M" "M" "M" "M" ...
 $ doe    : num  1990 1990 1990 1990 1990 1990 1990 1990 1990 1990 ...
 $ dob    : num  1940 1940 1940 1940 1940 1940 1940 1940 1940 1940 ...
 $ lex.Cst: chr  "NRA" "NRA" "NRA" "NRA" ...
    matshade(nd$tfi, cbind(ci.pred(mp, newdata = nd),
                       ci.pred(mx, newdata = nd)) * 100,
         plot = TRUE,
         type = "l", lwd = 3:4, col = c("black", "forestgreen"),
         log = "y", xlab = "Time since entry (years)",
         ylab = "ESRD rate (per 100 PY) for 50 year old men")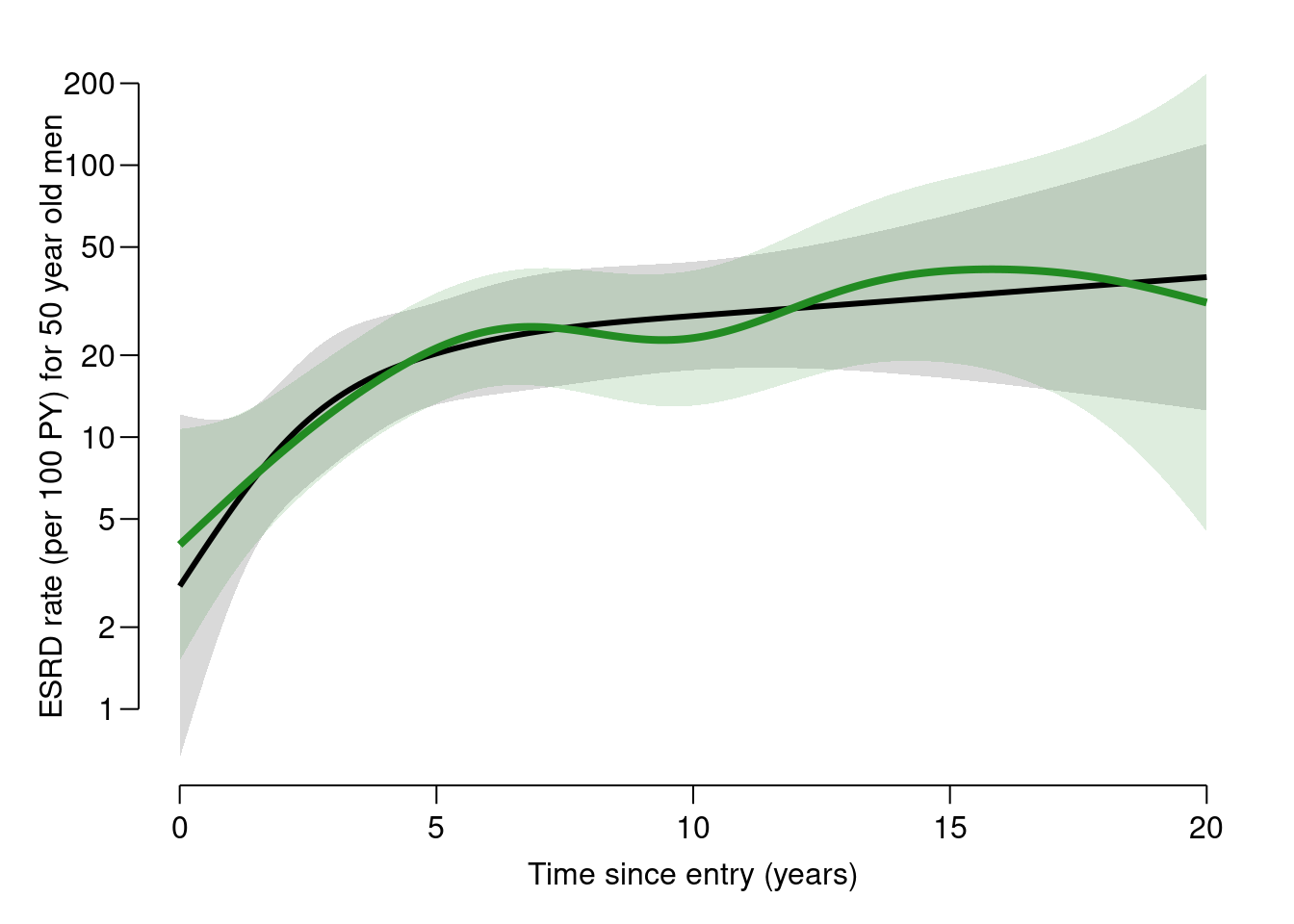

    Try to overlay with the corresponding prediction from the glm model using Ns.

## Prediction from the multistate model

If we want to make proper statements about the survival and disease
probabilities we must know not only how the occurrence of remission
influences the rate of death/ESRD, but we must also model the
occurrence rate of remission itself.

  1. The rates of ESRD were modelled by a Poisson model with effects of age and time since NRA — in the models mp and mx. But if we want to model whole process we must also model the remission rates transition from NRA to Rem, but the number of events is rather small so we restrict covariates in this model to only time since NRA and sex. Note that only the records that represent follow-up in the NRA state should be used; this is most easily done using the gam.Lexis function

    mr <- gam.Lexis(sLc, ~ s(tfi, k = 10) + sex,
                     from = "NRA",
                       to = "Rem")
    mgcv::gam Poisson analysis of Lexis object sLc with log link:
Rates for the transition:
NRA->Rem
    summary(mr)
    
Family: poisson 
Link function: log 

Formula:
cbind(trt(Lx$lex.Cst, Lx$lex.Xst) %in% trnam, Lx$lex.dur) ~ s(tfi, 
    k = 10) + sex

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -3.7025     0.2582 -14.339   <2e-16
sexF          0.9579     0.3728   2.569   0.0102

Approximate significance of smooth terms:
         edf Ref.df Chi.sq p-value
s(tfi) 1.013  1.025  0.066   0.813

R-sq.(adj) =  -5.65e-06   Deviance explained = 1.65%
UBRE = -0.96024  Scale est. = 1         n = 9952
    ci.exp(mr, pval = TRUE)
                 exp(Est.)       2.5%      97.5%            P
(Intercept) 0.02466174 0.01486718 0.04090901 1.254019e-46
sexF        2.60620470 1.25503844 5.41202779 1.019130e-02
s(tfi).1    1.00499489 0.89131271 1.13317662 9.351638e-01
s(tfi).2    0.99623769 0.80778743 1.22865188 9.718940e-01
s(tfi).3    0.99822247 0.91911268 1.08414140 9.663137e-01
s(tfi).4    1.00188999 0.89006998 1.12775801 9.750528e-01
s(tfi).5    0.99842904 0.92280785 1.08024715 9.687920e-01
s(tfi).6    0.99817367 0.90142303 1.10530865 9.719666e-01
s(tfi).7    1.00168704 0.92615949 1.08337380 9.663850e-01
s(tfi).8    0.99448155 0.68445450 1.44493689 9.768400e-01
s(tfi).9    0.94790052 0.63349476 1.41834700 7.946918e-01

    What is the remission rate-ratio between men and women?

  2. If we want to predict the probability of being in each of the three states using these estimated rates, we may resort to analytical calculations of the probabilities from the estimated rates, which is actually doable in this case, but which will be largely intractable for more complicated models. Alternatively we can simulate the life course for a large group of (identical) individuals through a model using the estimated rates. That will give a simulated cohort (in the form of a Lexis object), and we can then just count the number of persons in each state at each of a set of time points. This is accomplished using the function simLexis. The input to this is the initial status of the persons whose life-course we shall simulate, and the transition rates in suitable form:

    • Suppose we want predictions for men aged 50 at NRA. The input is in the form of a Lexis object (where lex.dur and lex.Xst will be ignored). Note that in order to carry over the time.scales and the time.since attributes, we construct the input object using subset to select columns, and NULL to select rows (see the example in the help file for simLexis):
    inL <- subset(sLc, select = 1:11)[NULL, ]
str(inL)
    Classes 'Lexis' and 'data.frame':   0 obs. of  11 variables:
 $ lex.id : int 
 $ per    : num 
 $ age    : num 
 $ tfi    : num 
 $ lex.dur: num 
 $ lex.Cst: Factor w/ 4 levels "NRA","Rem","ESRD",..: 
 $ lex.Xst: Factor w/ 4 levels "NRA","Rem","ESRD",..: 
 $ id     : num 
 $ sex    : Factor w/ 2 levels "M","F": 
 $ dob    : num 
 $ doe    : num 
 - attr(*, "time.scales")= chr [1:3] "per" "age" "tfi"
 - attr(*, "time.since")= chr [1:3] "" "" ""
 - attr(*, "breaks")=List of 3
  ..$ per: NULL
  ..$ age: NULL
  ..$ tfi: num [1:361] 0 0.0833 0.1667 0.25 0.3333 ...
    timeScales(inL)
    [1] "per" "age" "tfi"
    inL[1, "lex.id"] <- 1
inL[1, "per"] <- 2000
inL[1, "age"] <- 50
inL[1, "tfi"] <- 0
inL[1, "lex.Cst"] <- "NRA"
inL[1, "lex.Xst"] <- NA
inL[1, "lex.dur"] <- NA
inL[1, "sex"] <- "M"
inL[1, "doe"] <- 2000
inL[1, "dob"] <- 1950
inL <- rbind(inL, inL)
inL[2, "sex"] <- "F"
inL
     lex.id  per age tfi lex.dur lex.Cst lex.Xst id sex  dob  doe
      1 2000  50   0      NA     NRA    <NA> NA   M 1950 2000
      1 2000  50   0      NA     NRA    <NA> NA   F 1950 2000
    str(inL)
    Classes 'Lexis' and 'data.frame':   2 obs. of  11 variables:
 $ lex.id : num  1 1
 $ per    : num  2000 2000
 $ age    : num  50 50
 $ tfi    : num  0 0
 $ lex.dur: num  NA NA
 $ lex.Cst: Factor w/ 4 levels "NRA","Rem","ESRD",..: 1 1
 $ lex.Xst: Factor w/ 4 levels "NRA","Rem","ESRD",..: NA NA
 $ id     : num  NA NA
 $ sex    : Factor w/ 2 levels "M","F": 1 2
 $ dob    : num  1950 1950
 $ doe    : num  2000 2000
 - attr(*, "breaks")=List of 3
  ..$ per: NULL
  ..$ age: NULL
  ..$ tfi: num [1:361] 0 0.0833 0.1667 0.25 0.3333 ...
 - attr(*, "time.scales")= chr [1:3] "per" "age" "tfi"
 - attr(*, "time.since")= chr [1:3] "" "" ""

    The other input for the simulation is the models for the transitions. This is given as a list with an element for each transient state (that is NRA and Rem), each of which is again a list with names equal to the states that can be reached from the transient state. The content of the list will be glm objects, in this case the models we just fitted, describing the transition rates:

    Tr <- list("NRA" = list("Rem"  = mr,
                        "ESRD" = mx),
           "Rem" = list("ESRD(Rem)" = mx))

    With this as input we can now generate a cohort, using N=5 to simulate life course of 10 persons (5 for each set of starting values in inL):

    (iL <- simLexis(Tr, inL, N = 10))
     lex.id     per   age  tfi lex.dur lex.Cst   lex.Xst id sex  dob  doe cens
      1 2000.00 50.00 0.00    8.46     NRA      ESRD NA   M 1950 2000 2020
      2 2000.00 50.00 0.00    5.39     NRA       Rem NA   M 1950 2000 2020
      2 2005.39 55.39 5.39    0.67     Rem ESRD(Rem) NA   M 1950 2000 2020
      3 2000.00 50.00 0.00    2.58     NRA      ESRD NA   M 1950 2000 2020
      4 2000.00 50.00 0.00   10.50     NRA      ESRD NA   M 1950 2000 2020
      5 2000.00 50.00 0.00    1.81     NRA      ESRD NA   M 1950 2000 2020
      6 2000.00 50.00 0.00    1.21     NRA      ESRD NA   M 1950 2000 2020
      7 2000.00 50.00 0.00    5.69     NRA      ESRD NA   M 1950 2000 2020
      8 2000.00 50.00 0.00    4.83     NRA      ESRD NA   M 1950 2000 2020
      9 2000.00 50.00 0.00    2.94     NRA       Rem NA   M 1950 2000 2020
      9 2002.94 52.94 2.94    7.09     Rem ESRD(Rem) NA   M 1950 2000 2020
     10 2000.00 50.00 0.00    5.71     NRA      ESRD NA   M 1950 2000 2020
     11 2000.00 50.00 0.00    0.94     NRA       Rem NA   F 1950 2000 2020
     11 2000.94 50.94 0.94    0.96     Rem ESRD(Rem) NA   F 1950 2000 2020
     12 2000.00 50.00 0.00    4.30     NRA       Rem NA   F 1950 2000 2020
     12 2004.30 54.30 4.30    7.93     Rem ESRD(Rem) NA   F 1950 2000 2020
     13 2000.00 50.00 0.00    9.52     NRA      ESRD NA   F 1950 2000 2020
     14 2000.00 50.00 0.00    1.35     NRA      ESRD NA   F 1950 2000 2020
     15 2000.00 50.00 0.00   14.71     NRA      ESRD NA   F 1950 2000 2020
     16 2000.00 50.00 0.00    0.84     NRA       Rem NA   F 1950 2000 2020
     16 2000.84 50.84 0.84    7.49     Rem ESRD(Rem) NA   F 1950 2000 2020
     17 2000.00 50.00 0.00    7.41     NRA      ESRD NA   F 1950 2000 2020
     18 2000.00 50.00 0.00    6.65     NRA      ESRD NA   F 1950 2000 2020
     19 2000.00 50.00 0.00    9.94     NRA      ESRD NA   F 1950 2000 2020
     20 2000.00 50.00 0.00    3.38     NRA      ESRD NA   F 1950 2000 2020
    summary(iL, by = "sex")
    $M

Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA   0   2    8         0        10       10      49.12        10
  Rem   0   0    0         2         2        2       7.76         2
  Sum   0   2    8         2        12       12      56.87        10

$F

Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA   0   3    7         0        10       10      59.03        10
  Rem   0   0    0         3         3        3      16.38         3
  Sum   0   3    7         3        13       13      75.41        10

    What type of object have you got as iL?

  3. Now generate the life course of, say, 5,000 persons, and look at the summary. The system.time command is just to tell you how long it took, you may want to start with 500 just to see how long that takes.

    system.time(sM <- simLexis(Tr, inL, N = 500, t.range = 12))
       user  system elapsed 
  2.631   3.265   2.022 
    summary(sM, by = "sex")
    $M

Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA  40  65  395         0       500      460    2737.09       500
  Rem   0  42    0        23        65       23     472.77        65
  Sum  40 107  395        23       565      483    3209.86       500

$F

Transitions:
     To
From  NRA Rem ESRD ESRD(Rem)  Records:  Events: Risk time:  Persons:
  NRA  26 156  318         0       500      474    2486.11       500
  Rem   0  89    0        67       156       67    1085.27       156
  Sum  26 245  318        67       656      541    3571.38       500

    Why are there so many ESRD-events in the resulting data set?

  4. Now count how many persons are present in each state at each time for the first 10 years after entry (which is at age 50). This can be done by using nState. Try:

    nStm <- nState(subset(sM, sex == "M"), time.scale = "age", 
               at = seq(0, 10, 0.1), 
             from = 50)
nStf <- nState(subset(sM, sex == "F"), time.scale = "age", 
               at = seq(0, 10, 0.1), 
             from = 50)
head(nStf, 15)
          State
when   NRA Rem ESRD ESRD(Rem)
  50   500   0    0         0
  50.1 497   2    1         0
  50.2 488   8    4         0
  50.3 482  10    8         0
  50.4 473  16   11         0
  50.5 468  21   11         0
  50.6 463  25   12         0
  50.7 458  28   14         0
  50.8 454  30   16         0
  50.9 448  35   17         0
  51   446  36   17         1
  51.1 446  36   17         1
  51.2 437  40   22         1
  51.3 432  41   26         1
  51.4 428  44   27         1

    What is in the object nStf?

  5. With the counts of persons in each state at the designated time points (in nStm), compute the cumulative fraction over the states, arranged in order given by perm:

    ppm <- pState(nStm, perm = c(2, 1, 3, 4))
ppf <- pState(nStf, perm = c(2, 1, 3, 4))
head(ppf)
          State
when     Rem   NRA ESRD ESRD(Rem)
  50   0.000 1.000    1         1
  50.1 0.004 0.998    1         1
  50.2 0.016 0.992    1         1
  50.3 0.020 0.984    1         1
  50.4 0.032 0.978    1         1
  50.5 0.042 0.978    1         1
    tail(ppf)
          State
when     Rem   NRA  ESRD ESRD(Rem)
  59.5 0.208 0.340 0.906         1
  59.6 0.208 0.334 0.906         1
  59.7 0.206 0.328 0.904         1
  59.8 0.208 0.326 0.902         1
  59.9 0.208 0.322 0.902         1
  60   0.206 0.320 0.900         1

    What do the entries in ppf represent?

  6. Try to plot the cumulative probabilities using the plot method for pState objects: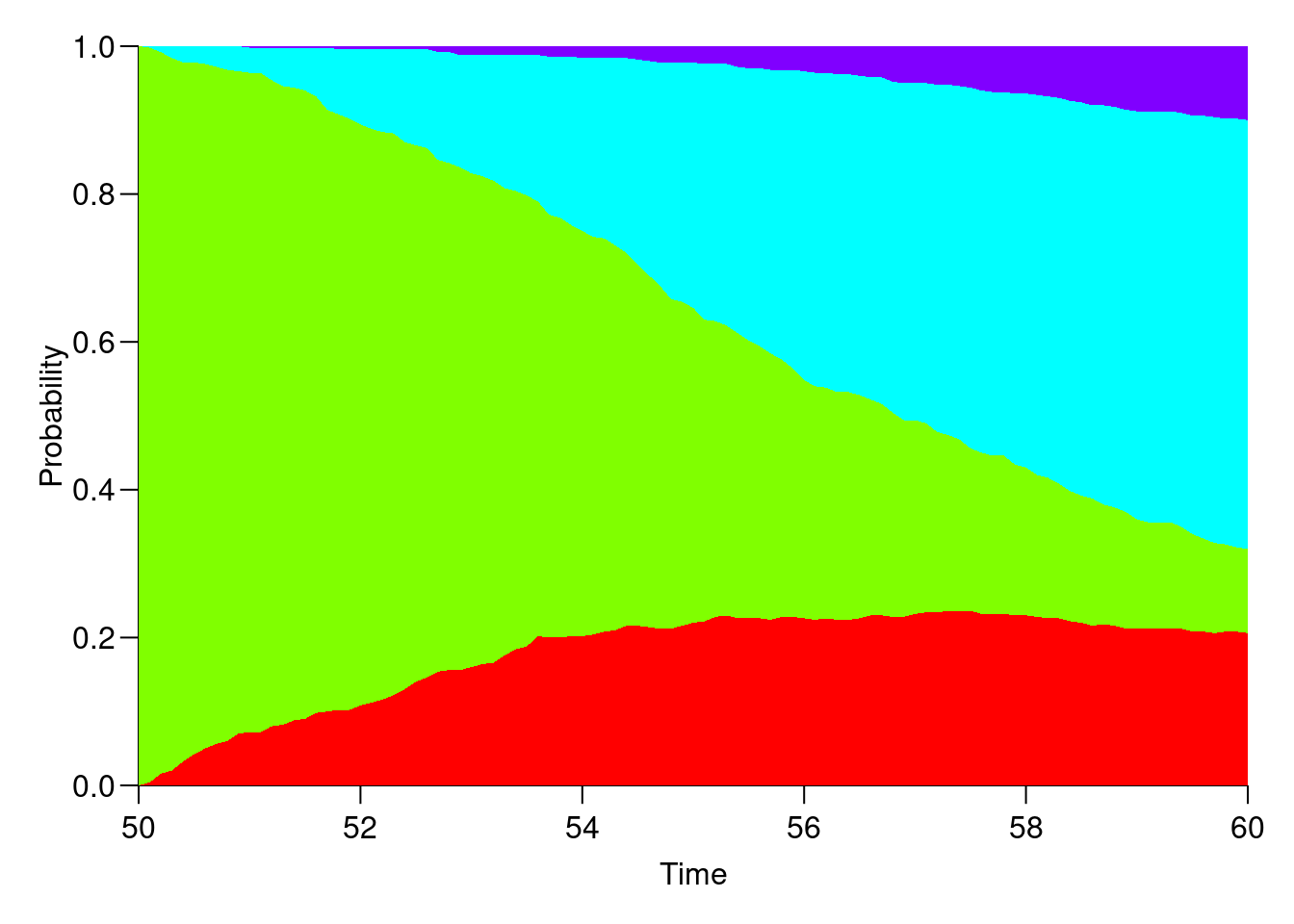

    plot(ppf)

    Is this useful?

  7. Now try to improve the plot so that it is easier to read, and easier to compare between men and women, for example:

    par(mfrow = c(1, 2))
# Men
plot(ppm, col = c("limegreen", "red", "#991111", "forestgreen"))
lines(as.numeric(rownames(ppm)), ppm[, "NRA"], lwd = 2)
text(59.5, 0.95, "Men", adj = 1, col = "white", font = 2, cex = 1.2)
axis(side = 4, at = 0:10 / 10)
axis(side = 4, at = 1:99 / 100, labels = NA, tck = -0.01)
# Women 
plot(ppf, col = c("limegreen", "red", "#991111", "forestgreen"),
          xlim = c(60, 50)) # inverted x-axis
lines(as.numeric(rownames(ppf)), ppf[, "NRA"], lwd = 2)
text(59.5, 0.95, "Women", adj = 0, col = "white", font = 2, cex = 1.2)
axis(side = 2, at = 0:10 / 10)
axis(side = 2, at = 1:99 / 100, labels = NA, tck = -0.01)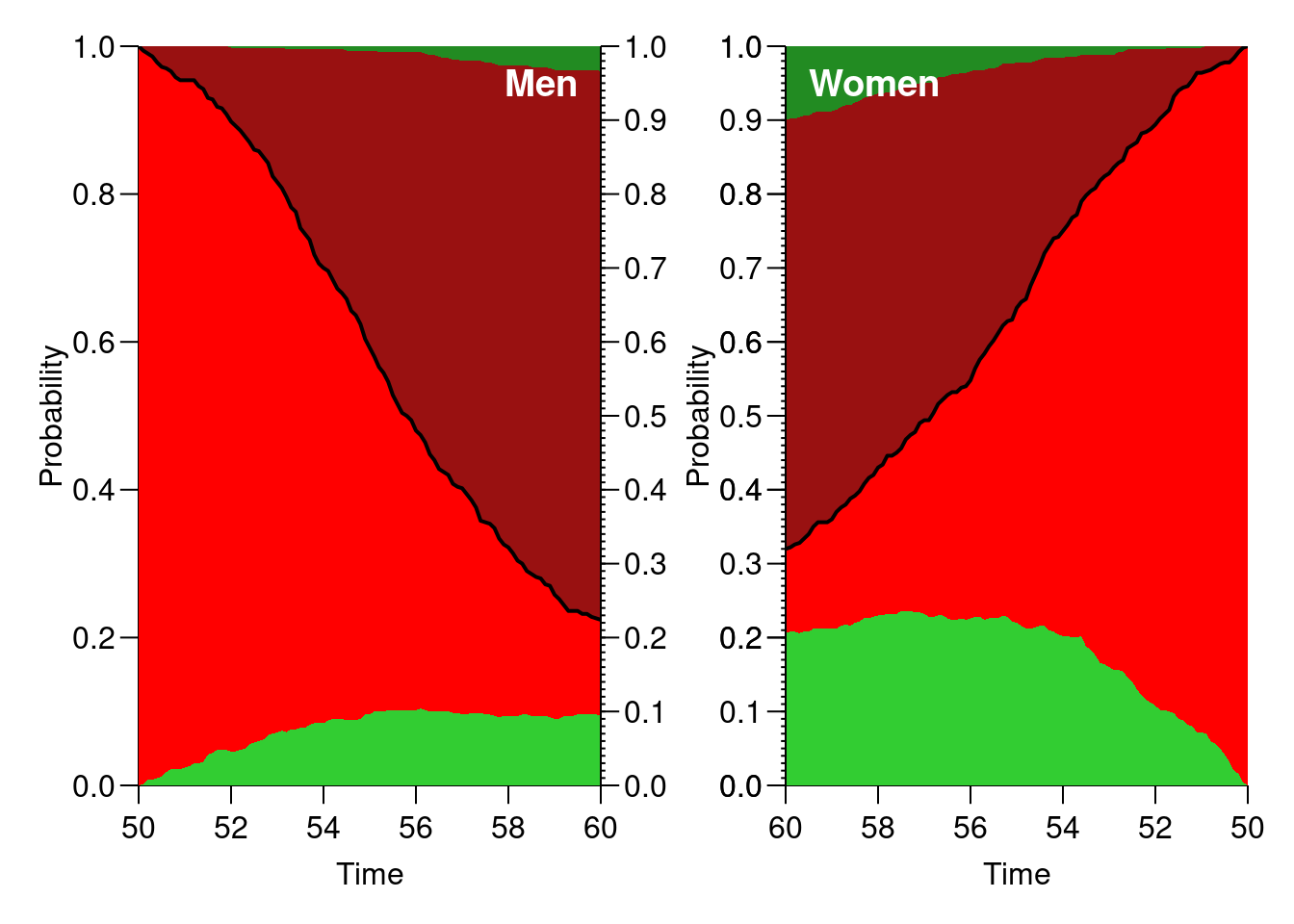

    What is the 10-year risk of remission for men and women respectively?