Chapter 12 Time-splitting, time-scales and SMR

This exercise is about mortaity among Danish Diabetes patients. It is based on the dataset DMlate, a random sample of 10,000 patients from the Danish Diabetes Register (scrambeled dates), all with date of diagnosis after 1994.

Start by loading the relevant packages:

library(Epi)
library(popEpi)
library(mgcv)
Loading required package: nlme
This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
library(tidyverse)
── Attaching core tidyverse packages ────────────────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ──────────────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::collapse()    masks nlme::collapse()
✖ dplyr::filter()      masks stats::filter()
✖ lubridate::is.Date() masks popEpi::is.Date()
✖ dplyr::lag()         masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Then load the data and take a look at the data:

data(DMlate)
str(DMlate)
'data.frame':   10000 obs. of  7 variables:
 $ sex  : Factor w/ 2 levels "M","F": 2 1 2 2 1 2 1 1 2 1 ...
 $ dobth: num  1940 1939 1918 1965 1933 ...
 $ dodm : num  1999 2003 2005 2009 2009 ...
 $ dodth: num  NA NA NA NA NA ...
 $ dooad: num  NA 2007 NA NA NA ...
 $ doins: num  NA NA NA NA NA NA NA NA NA NA ...
 $ dox  : num  2010 2010 2010 2010 2010 ...

You can get a more detailed explanation of the data by referring to the help page:

?DMlate

  1. Set up the dataset as a Lexis object with age, calendar time and duration of diabetes as timescales, and date of death as event. Make sure that you know what each of the arguments to Lexis mean:

    LL <- Lexis(entry = list(A = dodm - dobth, 
                         P = dodm, 
                       dur = 0),
             exit = list(P = dox),
      exit.status = factor(!is.na(dodth), 
                           labels = c("Alive", "Dead")),
             data = DMlate)
    NOTE: entry.status has been set to "Alive" for all.
NOTE: Dropping  4  rows with duration of follow up < tol

    Take a look at the first few lines of the resulting dataset, for example using head().

  2. Get an overview of the mortality by using stat.table to tabulate no. deaths, person-years (lex.dur) and the crude mortality rate by sex. Try:

    stat.table(sex,
           list(D = sum(lex.Xst == "Dead"),
                Y = sum(lex.dur),
             rate = ratio(lex.Xst == "Dead", 
                          lex.dur, 
                          1000)),
          margins = TRUE,
             data = LL)
     --------------------------------- 
 sex           D        Y    rate  
 --------------------------------- 
 M       1343.00 27614.21   48.63  
 F       1156.00 26659.05   43.36  

 Total   2499.00 54273.27   46.04  
 --------------------------------- 
    # stat.table is more versatile than xtabs:
xtabs(cbind(D = lex.Xst == "Dead",
            Y = lex.dur) 
      ~ sex, 
      data = LL)
    
sex        D        Y
  M  1343.00 27614.21
  F  1156.00 26659.05

  3. If we want to assess how mortality depends on age, calendar time and duration or how it relates to population mortality, we should in principle split the follow-up along all three time scales. In practice it is sufficient to split it along one of the time-scales and then use the value of each of the time-scales at the left endpoint of the intervals.

    Use splitLexis (or splitMulti from the popEpi package) to split the follow-up along the age-axis in sutiable intervals (here set to 1/2 year, but really immaterial as long as it is small):

    SL <- splitLexis(LL, 
                 breaks = seq(0, 125, 1 / 2), 
             time.scale = "A")
summary(SL)
    
Transitions:
     To
From     Alive Dead  Records:  Events: Risk time:  Persons:
  Alive 115974 2499    118473     2499   54273.27      9996

    How many records are now in the dataset? How many person-years? Compare to the original Lexis-dataset.

12.1 Age-specific mortality

  1. Now estimate age-specific mortality curves for men and women separately, using splines as implemented in gam. We use k = 20 to be sure to catch any irregularities by age.

    r.m <- mgcv::gam(cbind(lex.Xst == "Dead", lex.dur) ~ s(A, k = 20),
                 family = poisreg,
                   data = subset(SL, sex == "M"))

    Make sure you understand all the components on this modeling statement. Fit the same model for women.

    There is a convenient wrapper for this, exploiting the Lexis structure of data, but which does not have an update

    r.m <- gam.Lexis(subset(SL, sex == "M"), ~ s(A, k = 20))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "M") with log link:
Rates for the transition:
Alive->Dead
    r.f <- gam.Lexis(subset(SL, sex == "F"), ~ s(A, k = 20))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "F") with log link:
Rates for the transition:
Alive->Dead

  2. Now, extract the estimated rates by using the wrapper function ci.pred that computes predicted rates and confidence limits for these.

    glm.Lexis and gam.Lexis use the poisreg family that will return the rates in the (inverse) units in which the person-years were given; that is the units in which lex.dur is recorded.

    nd <- data.frame(A = seq(20, 90, 0.5))
p.m <- ci.pred(r.m, newdata = nd)
p.f <- ci.pred(r.f, newdata = nd)
str(p.m)
     num [1:141, 1:3] 0.00132 0.00137 0.00142 0.00147 0.00152 ...
 - attr(*, "dimnames")=List of 2
  ..$ : chr [1:141] "1" "2" "3" "4" ...
  ..$ : chr [1:3] "Estimate" "2.5%" "97.5%"

  3. Plot the predicted rates for men and women together - using for example matplot or matshade.

        par(mar = c(3.5,3.5,1,1),
        mgp = c(3,1,0) / 1.6,
        las = 1,
        bty = "n", 
       lend = "butt")
matplot(nd$A, cbind(p.m, p.f) * 1000,
        type = "l",
         col = rep(c("blue", "red"), each = 3),
         lwd = c(3, 1, 1),
         lty = 1,
         log = "y", yaxt = "n",
        xlab = "Age", 
        ylab = "Mortality per 1000 PY")
axis(side = 2, 
     at = ll <- outer( c(5, 10, 20), -1:1, function(x,y) x * 10^y),
     labels = ll)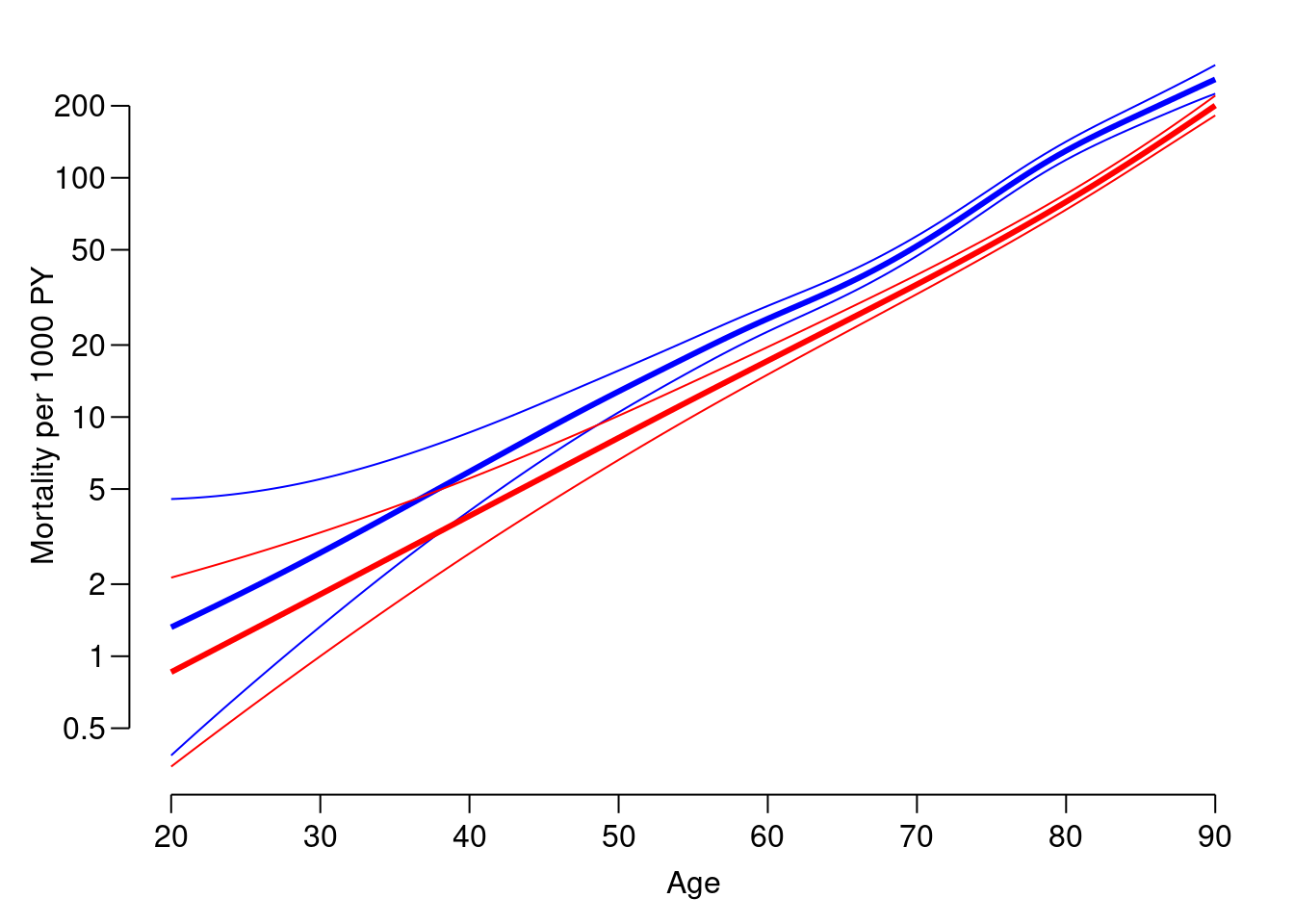

    Further time scales: period and duration

  4. We now want to model the mortality rates among diabetes patients also including current date and duration of diabetes, using penalized splines. Use the argument bs = "cr" to s() to get cubic splines instead of thin plate ("tp") splines which is the default.

    As before specify the model exploiting the Lexis class of the dataset, try:

    Mcr <- gam.Lexis(subset(SL, sex == "M"),
                 ~ s(A, bs = "cr", k = 10) +
                   s(P, bs = "cr", k = 10) +
                 s(dur, bs = "cr", k = 10))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "M") with log link:
Rates for the transition:
Alive->Dead
    summary(Mcr)
    
Family: poisson 
Link function: log 

Formula:
cbind(trt(Lx$lex.Cst, Lx$lex.Xst) %in% trnam, Lx$lex.dur) ~ s(A, 
    bs = "cr", k = 10) + s(P, bs = "cr", k = 10) + s(dur, bs = "cr", 
    k = 10)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.54074    0.04938   -71.7   <2e-16

Approximate significance of smooth terms:
         edf Ref.df  Chi.sq  p-value
s(A)   3.645  4.517 1013.20  < 2e-16
s(P)   1.024  1.048   17.58 3.48e-05
s(dur) 7.586  8.384   74.46  < 2e-16

R-sq.(adj) =  0.00333   Deviance explained = 9.87%
UBRE = -0.8054  Scale est. = 1         n = 60347

    Fit the same model for women as well. Are the models reasonably fitting?

    Fcr <- gam.Lexis(subset(SL, sex == "F"),
                 ~ s(A, bs = "cr", k = 10) +
                   s(P, bs = "cr", k = 10) +
                 s(dur, bs = "cr", k = 10))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "F") with log link:
Rates for the transition:
Alive->Dead
    summary(Fcr)
    
Family: poisson 
Link function: log 

Formula:
cbind(trt(Lx$lex.Cst, Lx$lex.Xst) %in% trnam, Lx$lex.dur) ~ s(A, 
    bs = "cr", k = 10) + s(P, bs = "cr", k = 10) + s(dur, bs = "cr", 
    k = 10)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.78483    0.05808  -65.17   <2e-16

Approximate significance of smooth terms:
         edf Ref.df Chi.sq  p-value
s(A)   2.667  3.366 988.49  < 2e-16
s(P)   1.904  2.391  20.08 0.000136
s(dur) 5.973  6.972  38.98  < 2e-16

R-sq.(adj) =  0.00417   Deviance explained = 11.1%
UBRE = -0.82405  Scale est. = 1         n = 58126

  5. Plot the estimated effects, using the default plot method for gam objects. Remember that there are three effects estimated, so it is useful set up a multi-panel display, and for the sake of comparability to set ylim to the same for men and women: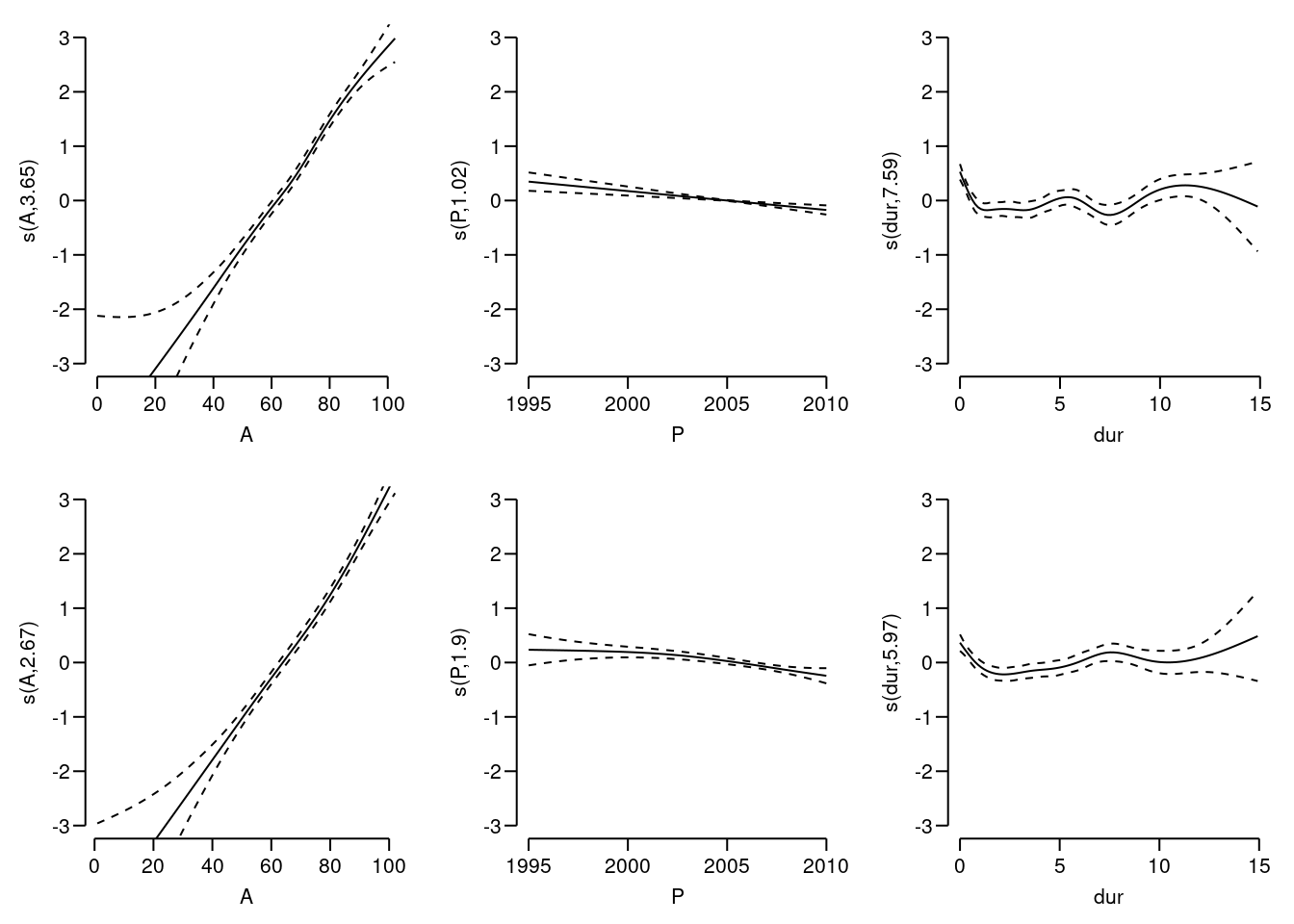

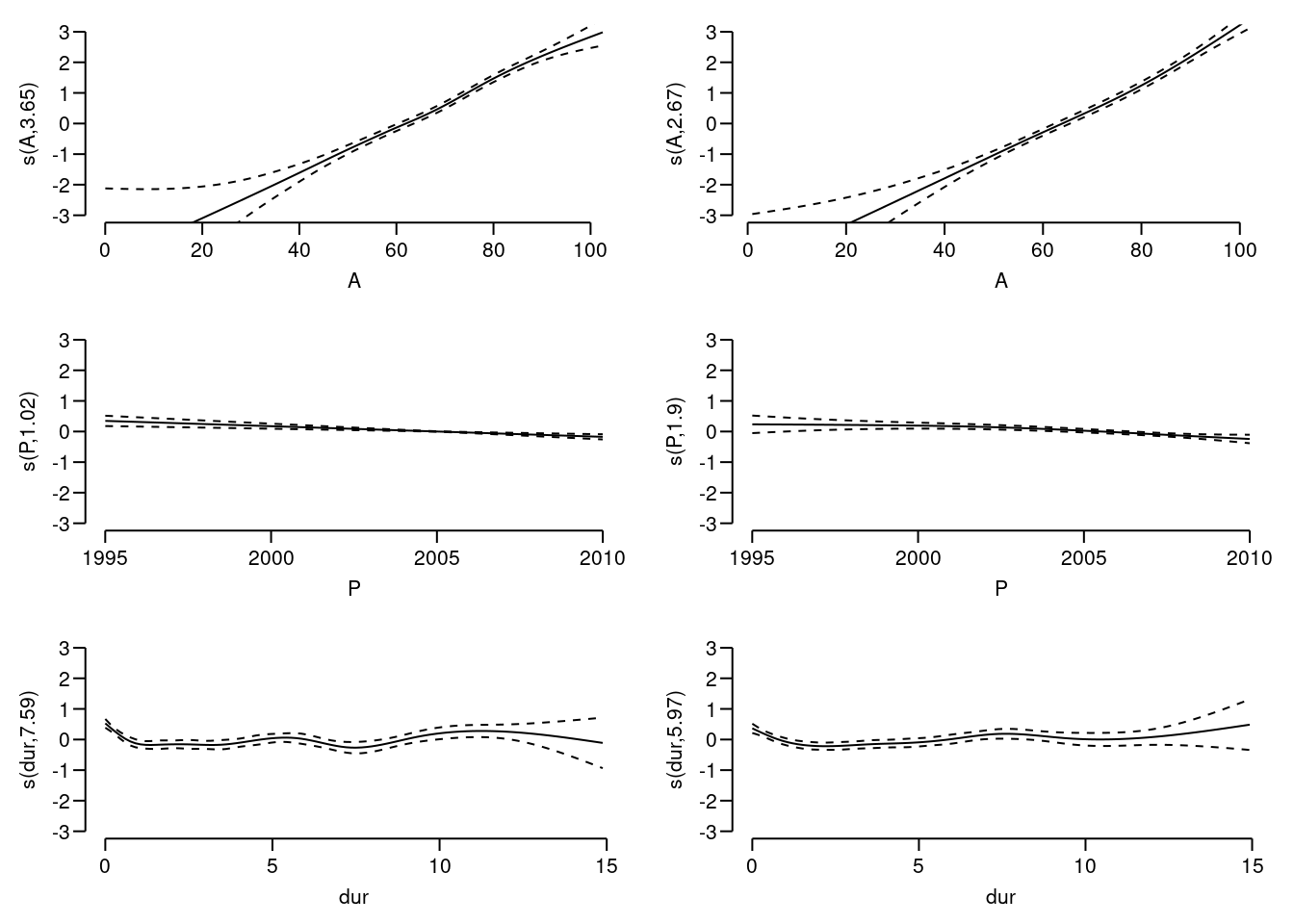    par(mfrow = c(2, 3))
plot(Mcr, ylim = c(-3, 3))
plot(Fcr, ylim = c(-3, 3))

    par(mfcol = c(3, 2))
plot(Mcr, ylim = c(-3, 3))
plot(Fcr, ylim = c(-3, 3))

    What is the absolute scale for these effects?

  6. Compare the fit of the naive model with just age and the three-factor models, using anova, e.g.:

    anova(Mcr, r.m, test = "Chisq")
    Analysis of Deviance Table

Model 1: cbind(trt(Lx$lex.Cst, Lx$lex.Xst) %in% trnam, Lx$lex.dur) ~ s(A, 
    bs = "cr", k = 10) + s(P, bs = "cr", k = 10) + s(dur, bs = "cr", 
    k = 10)
Model 2: cbind(trt(Lx$lex.Cst, Lx$lex.Xst) %in% trnam, Lx$lex.dur) ~ s(A, 
    k = 20)
  Resid. Df Resid. Dev      Df Deviance  Pr(>Chi)
1     60332      11717                           
2     60340      11812 -7.9484  -95.094 < 2.2e-16

    What do you conclude?

  7. The model we fitted has three time-scales: current age, current date and current duration of diabetes, so the effects that we report are not immediately interpretable, as they are (as in any kind of multiple regressions) to be interpreted as all else equal which they are not, as the three time scales advance simultaneously at the same pace.

    The reporting would therefore more naturally be on the mortality scale as a function of age, but showing the mortality for persons diagnosed in different ages, using separate displays for separate years of diagnosis. This is most easily done using the ci.pred function with the newdata = argument. So a person diagnosed in age 50 in 1995 will have a mortality measured in cases per 1000 PY as:

    pts <- seq(0, 12, 1/4)
nd <- data.frame(A = 50   + pts, 
                 P = 1995 + pts, 
               dur =        pts)
m.pr <- ci.pred(Mcr, newdata = nd)

    Note that because we used gam.Lexis which uses the poisreg family we need not specify lex.dur as a variable in the prediction data frame nd. Predictions will be rates in the same units as lex.dur (well, the inverse).

    Now take a look at the result from the ci.pred statement and construct prediction of mortality for men and women diagnosed in a range of ages, say 50, 60, 70, and plot these together in the same graph:

    cbind(nd, ci.pred(Mcr, newdata = nd))[1:10,]

  8. From figure it seems that the duration effect is over-modeled, so refit constraining the d.f. to 5:

    Mcr <- gam.Lexis(subset(SL, sex == "M"),
                 ~ s(A, bs = "cr", k = 10) +
                   s(P, bs = "cr", k = 10) +
                 s(dur, bs = "cr", k = 5))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "M") with log link:
Rates for the transition:
Alive->Dead
    Fcr <- gam.Lexis(subset(SL, sex == "F"),
                 ~ s(A, bs = "cr", k = 10) +
                   s(P, bs = "cr", k = 10) +
                 s(dur, bs = "cr", k = 5))
    mgcv::gam Poisson analysis of Lexis object subset(SL, sex == "F") with log link:
Rates for the transition:
Alive->Dead

    Plot the estimated rates from the revised models. What do you conclude from the plots?

12.2 SMR

The SMR is the Standardized Mortality Ratio, which is the mortality rate-ratio between the diabetes patients and the general population. In real studies we would subtract the deaths and the person-years among the diabetes patients from those of the general population, but since we do not have access to these, we make the comparison to the general population at large, i.e. also including the diabetes patients.

So we now want to include the population mortality rates as a fixed variable in the split dataset; for each record in the split dataset we attach the value of the population mortality for the relevant sex, and and calendar time.

This can be achieved in two ways: Either we just use the current split of follow-up time and allocate the population mortality rates for some suitably chosen (mid-)point of the follow-up in each, or we make a second split by date, so that follow-up in the diabetes patients is in the same classification of age and data as the population mortality table.

  1. We will use the former approach, using the dataset split in 6 month intervals, and then include as an extra variable the population mortality as available from the data set M.dk.

    First create the variables in the diabetes dataset that we need for matching with the population mortality data, that is sex and age and date at the midpoint of each of the intervals (or rather at a point 3 months after the left endpoint of the interval; recall we split the follow-up in 6 month intervals).

    We need to have variables of the same type when we merge, so we must transform the sex variable in M.dk to a factor, and must for each follow-up interval in the SL data have an age and a period variable that can be used in merging with the population data.

    str(SL)
    Classes 'Lexis' and 'data.frame':   118473 obs. of  14 variables:
 $ lex.id : int  1 1 1 1 1 1 1 1 1 1 ...
 $ A      : num  58.7 59 59.5 60 60.5 ...
 $ P      : num  1999 1999 2000 2000 2001 ...
 $ dur    : num  0 0.339 0.839 1.339 1.839 ...
 $ lex.dur: num  0.339 0.5 0.5 0.5 0.5 ...
 $ lex.Cst: Factor w/ 2 levels "Alive","Dead": 1 1 1 1 1 1 1 1 1 1 ...
 $ lex.Xst: Factor w/ 2 levels "Alive","Dead": 1 1 1 1 1 1 1 1 1 1 ...
 $ sex    : Factor w/ 2 levels "M","F": 2 2 2 2 2 2 2 2 2 2 ...
 $ dobth  : num  1940 1940 1940 1940 1940 ...
 $ dodm   : num  1999 1999 1999 1999 1999 ...
 $ dodth  : num  NA NA NA NA NA NA NA NA NA NA ...
 $ dooad  : num  NA NA NA NA NA NA NA NA NA NA ...
 $ doins  : num  NA NA NA NA NA NA NA NA NA NA ...
 $ dox    : num  2010 2010 2010 2010 2010 ...
 - attr(*, "breaks")=List of 3
  ..$ A  : num [1:251] 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 ...
  ..$ P  : NULL
  ..$ dur: NULL
 - attr(*, "time.scales")= chr [1:3] "A" "P" "dur"
 - attr(*, "time.since")= chr [1:3] "" "" ""
    SL$Am <- floor(SL$A + 0.25)
SL$Pm <- floor(SL$P + 0.25)
data(M.dk)
str(M.dk)
    'data.frame':   7800 obs. of  6 variables:
 $ A   : num  0 0 0 0 0 0 0 0 0 0 ...
 $ sex : num  1 2 1 2 1 2 1 2 1 2 ...
 $ P   : num  1974 1974 1975 1975 1976 ...
 $ D   : num  459 303 435 311 405 258 332 205 312 233 ...
 $ Y   : num  35963 34383 36099 34652 34965 ...
 $ rate: num  12.76 8.81 12.05 8.97 11.58 ...
 - attr(*, "Contents")= chr "Number of deaths and risk time in Denmark"
    M.dk <- transform(M.dk,
                  Am = A,
                  Pm = P,
                 sex = factor(sex, labels = c("M", "F")))
str(M.dk)
    'data.frame':   7800 obs. of  8 variables:
 $ A   : num  0 0 0 0 0 0 0 0 0 0 ...
 $ sex : Factor w/ 2 levels "M","F": 1 2 1 2 1 2 1 2 1 2 ...
 $ P   : num  1974 1974 1975 1975 1976 ...
 $ D   : num  459 303 435 311 405 258 332 205 312 233 ...
 $ Y   : num  35963 34383 36099 34652 34965 ...
 $ rate: num  12.76 8.81 12.05 8.97 11.58 ...
 $ Am  : num  0 0 0 0 0 0 0 0 0 0 ...
 $ Pm  : num  1974 1974 1975 1975 1976 ...

    Then match the rates from M.dk into SL; sex, Am and Pm are the common variables, and therefore the match is on these variables:

    SLr <- merge(SL, 
             M.dk[, c("sex", "Am", "Pm", "rate")])
dim(SL)
    [1] 118473     16
    dim(SLr)
    [1] 118454     17

    This merge (remember to ?merge!) only takes rows that have information from both datasets, hence the slightly fewer rows in SLr than in SL.

    • Compute the expected number of deaths as the person-time multiplied (lex.dur) by the corresponding population rate, and put it in a new variable, E, say (Expected). Use stat.table to make a table of observed, expected and the ratio (SMR) by age (suitably grouped, look for cut) and sex.

  2. Fit a poisson model with sex as the explanatory variable and log-expected as offset to derive the SMR (and c.i.). Some of the population mortality rates are 0, so you need to exclude those records from the analysis.

    msmr <- glm((lex.Xst == "Dead") ~ sex - 1,
            offset = log(E),
            family = poisson,
              data = subset(SLr, E > 0))
ci.exp(msmr)
         exp(Est.)     2.5%    97.5%
sexM  1.685699 1.597881 1.778344
sexF  1.541922 1.455442 1.633540

    Do you recognize the numbers?

    • The same model can be fitted a bit simpler by the poisreg family, try:
    msmr <- glm(cbind(lex.Xst == "Dead", E) ~ sex - 1, 
            family = poisreg,
              data = subset(SLr, E > 0))
ci.exp(msmr)
         exp(Est.)     2.5%    97.5%
sexM  1.685699 1.597881 1.778344
sexF  1.541922 1.455441 1.633541

    We can assess the ratios of SMRs between men and women by using the ctr.mat argument which should be a matrix:

    (CM <- rbind(M = c(1, 0),
             W = c(0, 1),
         "M/F" = c(1, -1)))
        [,1] [,2]
M      1    0
W      0    1
M/F    1   -1
    round(ci.exp(msmr, ctr.mat = CM), 2)
        exp(Est.) 2.5% 97.5%
M        1.69 1.60  1.78
W        1.54 1.46  1.63
M/F      1.09 1.01  1.18

    What do you conclude about the mortality rates among men and women?

12.3 SMR modeling

  1. Now model the SMR using age and date of diagnosis and diabetes duration as explanatory variables, including the expected-number instead of the person-years, using separate models for men and women.

    Note that you cannot use gam.Lexis from the code you used for fitting models for the rates, you need to use gam with the poisreg family. And remember to exclude those units where no deaths in the population occur (that is where the population mortality rate is 0).

    Msmr <- gam(cbind(lex.Xst == "Dead", E) 
            ~ s(  A, bs = "cr", k = 5) +
              s(  P, bs = "cr", k = 5) +
              s(dur, bs = "cr", k = 5),
            family = poisreg,
              data = subset(SLr, E > 0 & sex == "M"))
ci.exp(Msmr)
                exp(Est.)      2.5%     97.5%
(Intercept) 2.1667053 2.0001046 2.3471833
s(A).1      0.5960527 0.5181962 0.6856068
s(A).2      0.8927331 0.8650901 0.9212594
s(A).3      0.3663506 0.2818154 0.4762435
s(A).4      0.4587803 0.3763049 0.5593320
s(P).1      0.9893048 0.9732835 1.0055898
s(P).2      0.9608720 0.9085181 1.0162428
s(P).3      0.9027294 0.7825209 1.0414040
s(P).4      0.9173557 0.8132938 1.0347323
s(dur).1    0.6581828 0.5769629 0.7508362
s(dur).2    0.8446645 0.7613599 0.9370838
s(dur).3    0.7830215 0.6916313 0.8864877
s(dur).4    1.8176744 1.1041338 2.9923368
    Fsmr <- update(Msmr, data = subset(SLr, E > 0 & sex == "F"))

    Plot the estimated smooth effects for both men and women using e.g. plot.gam. What do you see?

  2. Plot the predicted SMRs from the models for men and women diagnosed in ages 50, 60 and 70 as you did for the rates. What do you see?

    par(mfrow = c(1,1))
n50 <- nd
n60 <- mutate(n50, A = A + 10)
n70 <- mutate(n50, A = A + 20)
head(n70)
          A       P  dur
1 70.00 1995.00 0.00
2 70.25 1995.25 0.25
3 70.50 1995.50 0.50
4 70.75 1995.75 0.75
5 71.00 1996.00 1.00
6 71.25 1996.25 1.25
    matshade(n50$A, cbind(ci.pred(Msmr, n50),
                      ci.pred(Fsmr, n50)), plot = TRUE,
         col = c("blue", "red"), lwd = 3,
         ylim = c(0.5, 5), log  = "y", xlim = c(50, 80))
matshade(n60$A, cbind(ci.pred(Msmr, n60),
                      ci.pred(Fsmr, n60)),
         col = c("blue", "red"), lwd = 3)
matshade(n70$A, cbind(ci.pred(Msmr, n70),
                      ci.pred(Fsmr, n70)),
         col = c("blue", "red"), lwd = 3)
abline(h = 1)
abline(v = 50 + 0:5, lty = 3, col = "gray")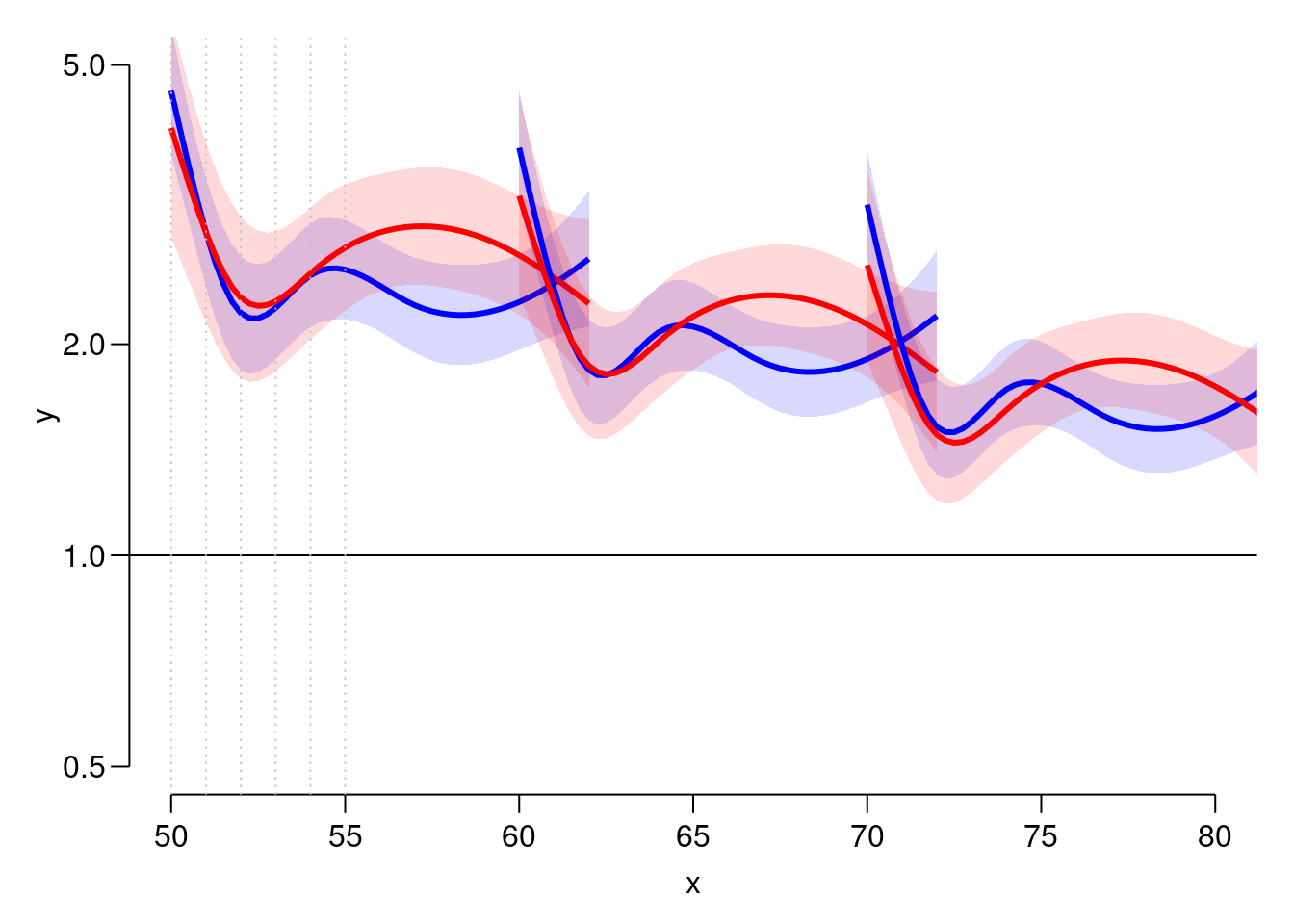

    Describe the shapes of the curves. What aspects of the shapes are induced by the model ?

  3. Try to simplify the model to one with a simple sex effect, separate linear effects of age and date of follow-up for each sex, and a smooth effect of duration common for both sexes, giving an estimate of the change in SMR by age and calendar time.

    Bsmr <- gam(cbind(lex.Xst == "Dead", E) 
            ~ sex / A +
              sex / P +
              s(dur, bs = "cr", k = 5),
            family = poisreg,
              data = subset(SLr, E > 0))
round(ci.exp(Bsmr)[-1,], 3)
             exp(Est.)  2.5%        97.5%
sexF     52149.525 0.000 2.375788e+23
sexM:A       0.981 0.977 9.860000e-01
sexF:A       0.980 0.975 9.860000e-01
sexM:P       0.987 0.972 1.002000e+00
sexF:P       0.981 0.965 9.980000e-01
s(dur).1     0.663 0.601 7.320000e-01
s(dur).2     0.861 0.795 9.310000e-01
s(dur).3     0.885 0.805 9.740000e-01
s(dur).4     1.412 0.945 2.111000e+00

    How much does SMR change by each year of age? And by each calendar year?

    What is the meaning of the sexF parameter?

  4. Use your previous code to plot the predicted mortality from this model too. Are the predicted SMR curves credible?

    m50 <- mutate(n50, sex = "M")
f50 <- mutate(n50, sex = "F")
m60 <- mutate(m50, A = A + 10)
f60 <- mutate(f50, A = A + 10)
m70 <- mutate(m50, A = A + 20)
f70 <- mutate(f50, A = A + 20)
matshade(n50$A, cbind(ci.pred(Bsmr, m50),
                      ci.pred(Bsmr, f50)), plot = TRUE,
         col = c("blue", "red"), lwd = 3,
         ylim = c(0.5, 5), log  = "y", xlim = c(50, 80))
matshade(n60$A, cbind(ci.pred(Bsmr, m60),
                      ci.pred(Bsmr, f60)),
         col = c("blue", "red"), lwd = 3)
matshade(n70$A, cbind(ci.pred(Bsmr, m70),
                      ci.pred(Bsmr, f70)),
         col = c("blue", "red"), lwd = 3)
abline(h = 1)
abline(h = 1:5, lty = 3, col = "gray")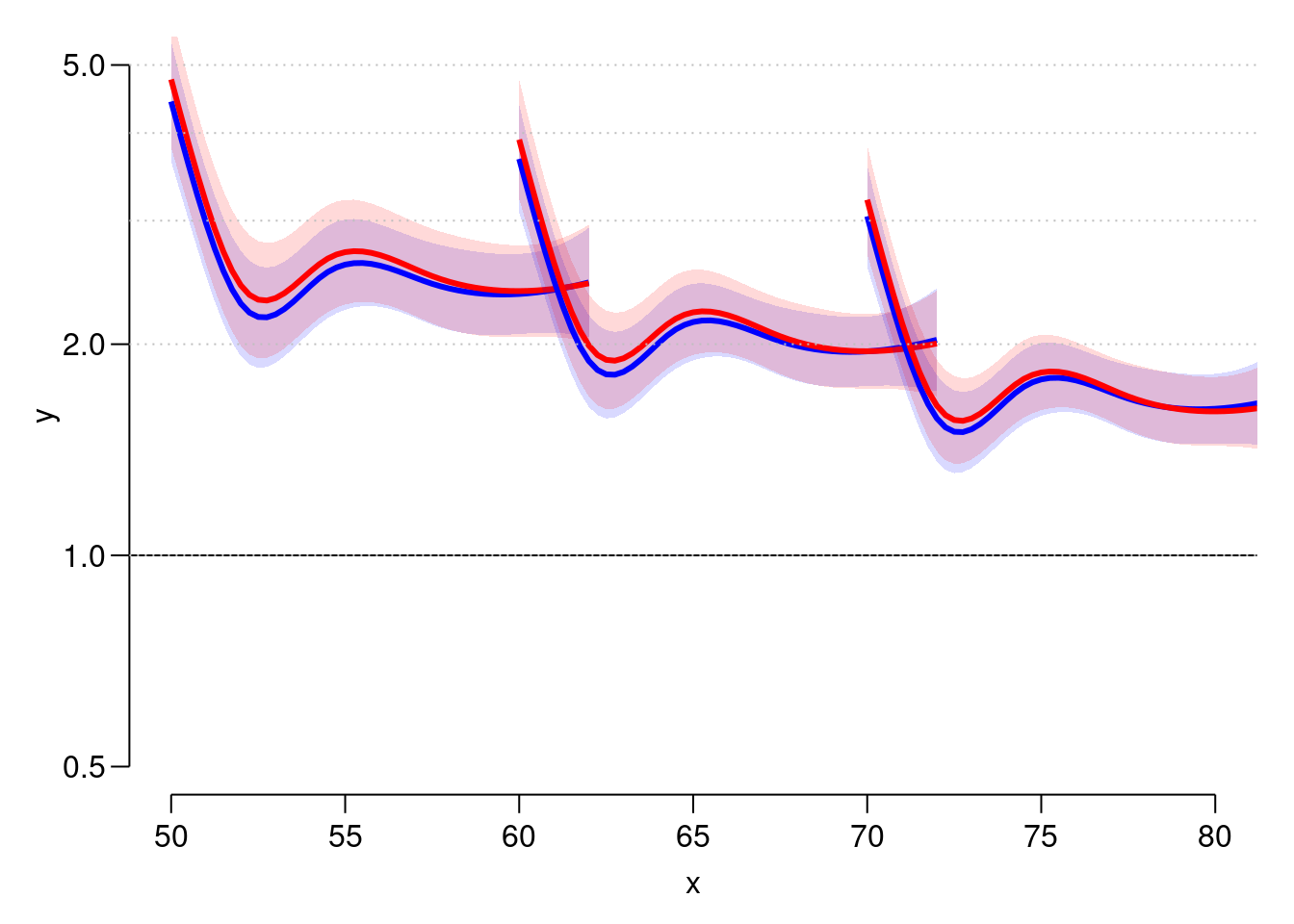

    What is your conclusion about SMR for diabetes patients relative to the general popuation?